Uma esfera homogênea de massa e raio está conectada sem atrito a um eixo vertical passando no seu centro. A esfera está inicialmente em repouso com um besouro de massa parado na sua linha equatorial. Num dado instante o besouro começa a se mover ao longo da linha equatorial com velocidade de módulo constante .
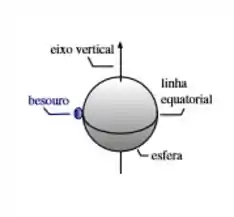
(a) Sabendo que existe atrito entre a esfera e o besouro, o momento angular total do sistema ‘esfera + besouro’ ´e conservado? Justifique.
(b) Calcule o momento de inércia do sistema ‘esfera besouro’ em relação ao eixo mencionado. Dado: Momento de inércia de uma esfera homogênea de massa e raio ao redor de um eixo passando no seu centro: .
(c) Calcule a velocidade angular que a esfera adquire quando o besouro se movimenta.
Passo 1
a) Sim. O torque resultante é nulo, pois as forças de atrito entre a esfera e o besouro são internas, de modo que a soma dos torques externos é zero. E como:
O momento angular não varia.
Passo 2
b) Aqui é bem simples, basta somar o momento de inércia com o do besouro em relação ao mesmo eixo.
Passo 3
c) Usando a conservação do momento angular(provada no item (a)), temos:
Como o sistema estava em repouso no início,
No entanto:
Portanto:
O sinal de menos mostra que a esfera roda pro sentido contrário da velocidade do besouro.
Resposta
a) Sim
b)
c)