P3 de Física 1 da UnB - 2017.1

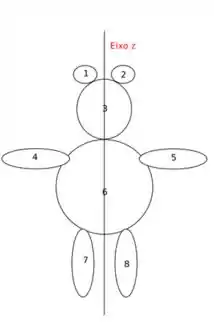
Um veículo possui massa de tonelada e quatro rodas de liga leve de massa cada e diâmetro de . Outro veículo idêntico possui rodas de aço de de diâmetro, e mesma massa das de liga leve. Compare a velocidade dos veículos ao final de uma descida de de comprimento e inclinação de . Suponha que ambos veículos tenham velocidade inicial nula.

O momento de inércia, possui propriedades similares às do centro de massa, pois ambos são dados na forma de uma integral. Sendo assim, no cálculo do momento de inércia é possível dividir o domínio de integração em subdomínios e posteriormente somar o resultado. Por exemplo, para a figura abaixo (um urso”), basta calcular o momento de inércia de cada uma das sub-regiões numeradas de a em relação ao eixo , e depois somar o resultado:

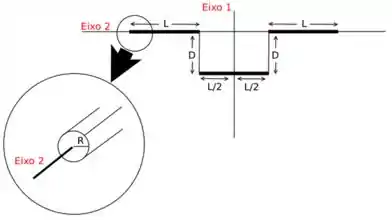
Sabendo disto, calcule o momento de inércia da figura abaixo em relação aos eixos e , supondo que as barras delgadas possuem massa desprezível e que as barras grossas possuem massa , são homogêneas e possuem secção reta circular de raio .

Dados: momento de inércia de um cilindro homogêneo de massa em relação ao eixo que passa pelo centro de sua secção reta de raio e pelo seu centro de massa: momento de inércia de uma barra homogênea de massa e comprimento em relação ao eixo que é perpendicular à extensão da barra e passa pelo seu centro de massa:

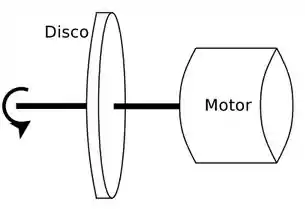
Em um motor elétrico típico, a curva de torque é aproximadamente constante na faixa de rotações de trabalho do motor. Suponha que o eixo deste motor está conectado à uma roda de massa , em formato de cilindro. Sabendo que o torque do motor é dado por , obtenha a aceleração angular e a velocidade angular em função do tempo .

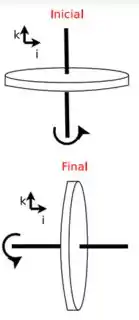
Um disco de raio e massa gira livremente com velocidade angular em torno de um eixo vertical que passa pelo seu centro de massa. Pela ação de um torque, o eixo de rotação é alterado para a horizontal em um intervalo de tempo , conforme a figura abaixo. Sabendo que o módulo da velocidade angular do disco manteve-se constante durante a aplicação do torque, mostre que o módulo do torque médio aplicado é dado por: