Listas de Exercícios Física 1 - UnB de Física 1 da UnB - Lista 7 - Trabalho e Energia

O coração humano é uma bomba potente e extermamente confiável. A cada dia ele recebe e descarrega cerca de de sangue. Suponha que o trabalho realizado pelo coração seja igual ao trabalho necessário para ele elevar essa quantidade de sangue até uma altura igual à altura média de uma mulher norteamericana (). A densidade (massa por unidade de volume) do sangue é igual a .

a) Qual é o trabalho realizado pelo coração em um dia?

O coração humano é uma bomba potente e extermamente confiável. A cada dia ele recebe e descarrega cerca de de sangue. Suponha que o trabalho realizado pelo coração seja igual ao trabalho necessário para ele elevar essa quantidade de sangue até uma altura igual à altura média de uma mulher norteamericana (). A densidade (massa por unidade de volume) do sangue é igual a .

b) Qual a potência de saída em watts?

Uma caixa desliza sobre uma superfície horizontal com velocidade escalar de quando, no ponto , encontra uma área áspera. Na área áspera, o coeficiente de atrito não é constante, mas se inicia a em e aumenta linearmente conforme ultrapassa , atingindo um valor de a após o ponto .

a) Use o teorema do trabalho-energia cinética para achar a distância percorrida por essa caixa antes de parar.

Uma caixa desliza sobre uma superfície horizontal com velocidade escalar de quando, no ponto , encontra uma área áspera. Na área áspera, o coeficiente de atrito não é constante, mas se inicia a em e aumenta linearmente conforme ultrapassa , atingindo um valor de a após o ponto .

b) Qual é o coeficiente de atrito no ponto de parada?

Uma caixa desliza sobre uma superfície horizontal com velocidade escalar de quando, no ponto , encontra uma área áspera. Na área áspera, o coeficiente de atrito não é constante, mas se inicia a em e aumenta linearmente conforme ultrapassa , atingindo um valor de a após o ponto .

c) Qual a distância a caixa percorreria, caso o coeficiente de atrito não aumentasse, mas, em vez disso, tivesse o valor constante de 0.100?

Considere uma certa mola que não obedece rigorosamente à lei de Hooke. Uma das extremidades da mola é mantida fixa. Para manter a mola comprimida, ou esticada a uma distância , é necessário aplicar uma força ao longo do eixo com módulo dado por . Aqui, , e . Note que para , a mola está esticada e para a mola está comprimida.

a) Qual o trabalho necessário para esticar essa mola a partir de seu comprimento sem deformação?

Considere uma certa mola que não obedece rigorosamente à lei de Hooke. Uma das extremidades da mola é mantida fixa. Para manter a mola comprimida, ou esticada a uma distância , é necessário aplicar uma força ao longo do eixo com módulo dado por . Aqui, , e . Note que para , a mola está esticada e para a mola está comprimida.

b) Qual o trabalho necessário para comprimir essa mola a partir do seu comprimento sem deformação? Explique porque, em termos da dependência de com .(Muitas molas reais se comportam qualitativamente do mesmo modo.)

Um pequeno bloco com massa de está ligado a um fio que passa através de um buraco em uma superfície horizontal sem atrito (figura abaixo). Inicialmente, o bloco gira a uma distância de do buraco com uma velocidade de . A seguir, o fio é puxado para baixo, fazendo o raio do círculo encurtar para . Nesta nova distância verifica-se que sua velocidade passa para .

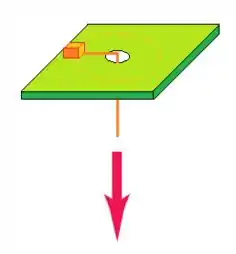
a) Qual era a tensão no fio quando o bloco possuía velocidade final ?

Um pequeno bloco com massa de está ligado a um fio que passa através de um buraco em uma superfície horizontal sem atrito (figura abaixo). Inicialmente, o bloco gira a uma distância de do buraco com uma velocidade de . A seguir, o fio é puxado para baixo, fazendo o raio do círculo encurtar para . Nesta nova distância verifica-se que sua velocidade passa para .

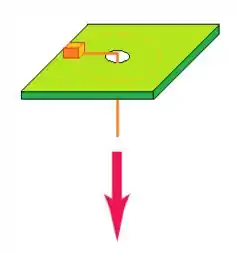
b) Qual era a tensão no fio quando o bloco possuía velocidade final ?

Um pequeno bloco com massa de está ligado a um fio que passa através de um buraco em uma superfície horizontal sem atrito (figura abaixo). Inicialmente, o bloco gira a uma distância de do buraco com uma velocidade de . A seguir, o fio é puxado para baixo, fazendo o raio do círculo encurtar para . Nesta nova distância verifica-se que sua velocidade passa para .

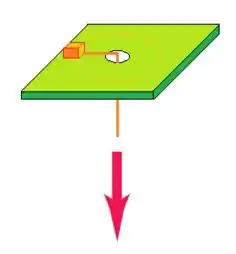
c) Qual foi o trabalho realizado pela pessoa que puxou o fio?

Um próton com massa igual a é impulsionado com uma velocidade inicial de diretamente contra um núcleo de urânio situado a uma distância de . O próton é repelido pelo núcleo de urânio com uma força de módulo , onde é a distância entre as duas partículas e . Suponha que o núcleo de urânio permaneça em repouso.

a) Qual é a velocidade do próton quando ele está a uma distância de do núcleo de urânio?

Um próton com massa igual a é impulsionado com uma velocidade inicial de diretamente contra um núcleo de urânio situado a uma distância de . O próton é repelido pelo núcleo de urânio com uma força de módulo , onde é a distância entre as duas partículas e . Suponha que o núcleo de urânio permaneça em repouso.

b) À medida que o próton se aproxima do núcleo de urânio, a força de repulsão faz sua velocidade diminuir até ele ficar momentaneamente em repouso, depois passando a se afastar do núcleo de urânio. Qual é a distância mínima entre o próton e o núcleo de urânio?

Um próton com massa igual a é impulsionado com uma velocidade inicial de diretamente contra um núcleo de urânio situado a uma distância de . O próton é repelido pelo núcleo de urânio com uma força de módulo , onde é a distância entre as duas partículas e . Suponha que o núcleo de urânio permaneça em repouso.

c) Qual é a velocidade do próton quando ele está novamente a uma distância de do núcleo de urânio?

Um bloco de gelo com massa de está inicialmente em repouso sobre uma superfície horizontal sem atrito. A seguir, um trabalhador aplica uma força horizontal sobre ele. Como resultado, o bloco se move ao longo do eixo de tal modo que sua posição em função do tempo é dada por , onde e .

a) Calcule a velocidade do bloco quando

Um bloco de gelo com massa de está inicialmente em repouso sobre uma superfície horizontal sem atrito. A seguir, um trabalhador aplica uma força horizontal sobre ele. Como resultado, o bloco se move ao longo do eixo de tal modo que sua posição em função do tempo é dada por , onde e .

b) Calcule o módulo de quando .

Um bloco de gelo com massa de está inicialmente em repouso sobre uma superfície horizontal sem atrito. A seguir, um trabalhador aplica uma força horizontal sobre ele. Como resultado, o bloco se move ao longo do eixo de tal modo que sua posição em função do tempo é dada por , onde e .

c) Calcule o trabalho realizado pela força durante os primeiros do movimento.

Você e sua bicicleta possuem massa total igual a . Quando você atinge a base de uma ponte, está se deslocando com uma velocidade de . No topo da ponte você subiu uma distância vertical de e sua velocidade diminuiu para . Despreze o trabalho realizado pelo atrito e qualquer ineficiência na bicicleta ou em suas pernas.

a) Qual o trabalho total realizado sobre você e sua bicicleta quando você vai da base ao topo da ponte?

Você e sua bicicleta possuem massa total igual a . Quando você atinge a base de uma ponte, está se deslocando com uma velocidade de . No topo da ponte você subiu uma distância vertical de e sua velocidade diminuiu para . Despreze o trabalho realizado pelo atrito e qualquer ineficiência na bicicleta ou em suas pernas.

b) Qual o trabalho realizado pela força que você aplica sobre os pedais?

Um professor de física está sentado em sua cadeira, que desliza sobre rolamentos sem atrito, sendo empurrado para cima de um plano inclinado a acima da horizontal. A massa total do professor com sua cadeira é igual a . Ele é empurrado ao longo do plano inclinado por um grupo de alunos que juntos exercem uma força horizontal constante de . O professor possuía uma velocidade de na base da rampa. Use o teorema do trabalho-energia cinética para calcular sua velocidade no topo da rampa.

Um bloco de se move com uma velocidade de sobre uma superfície horizontal sem atrito, dirigindo-se contra uma mola cuja constante elástica é dada por e que possui uma de suas extremidades presa a uma parede (ver figura abaixo).

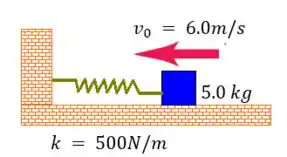
a) Calcule a distância máxima que a mola pode ser comprimida.

Um bloco de se move com uma velocidade de sobre uma superfície horizontal sem atrito, dirigindo-se contra uma mola cuja constante elástica é dada por e que possui uma de suas extremidades presa a uma parede (ver figura abaixo).

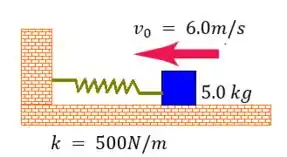
b) Se a distância máxima que a mola pudesse ser comprimida fosse de , qual seria o valor máximo de ?

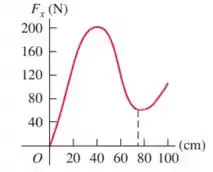
A figura abaixo mostra como a força exercida pelo fio de um arco varia em função da distância em que a flecha é puxada para trás (o comprimento de deformação). Suponha que a mesma força seja fornecida para a flecha que se move para frente quando o fio é liberado. A deformação máxima para esse arco corresponde a um comprimento de deformação igual a . Se o arco atira uma flecha de quando ele está submetido a uma deformação máxima, qual é a velocidade da flecha quando ela abandona o arco?