UNB, UnB - Gama, Física 1, P3 - 2017.1, Questão 3
Em um motor elétrico típico, a curva de torque é aproximadamente constante na faixa de rotações de trabalho do motor. Suponha que o eixo deste motor está conectado à uma roda de massa , em formato de cilindro. Sabendo que o torque do motor é dado por , obtenha a aceleração angular e a velocidade angular em função do tempo .
Passo 1
Eaí gente, tudo certinho com vocês?
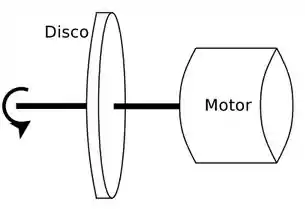
Nessa questão temos um motor que está fazendo um disco girar. O torque exercido pelo motor é constante e vale:
Precisamos determinar a aceleração angular do disco e a sua velocidade angular em função do tempo, sabendo que ele possui massa .
Embora não tenha sido dado no enunciado, vamos considerar também que o raio desse disco é , beleza?
Bom, pra resolver essa questão tem duas expressões bem importantes que devemos lembrar:
A segunda expressão é válida se a aceleração angular for constante.
Sabendo disso, vamos utilizar o fato do torque ser constante junto com as duas expressões acima para determinar a aceleração e velocidade angular 😊
Passo 2
Como o torque imprimido pelo motor no disco vale , podemos escrever que:
O momento de inércia de um disco é dado por:
Substituindo na expressão, temos:
Olha aí! Encontramos a aceleração angular. E, como todos os parâmetros que ela depende são constantes, podemos afirmar que a aceleração angular do disco é constante.
Passo 3
Como vimos que é constante, podemos usar a expressão do passo pra determinar a velocidade angular em função do tempo:
Considerando que antes do motor ser ligado o disco estava parado, podemos dizer que . Assim:
Substituindo o valor de calculado:
Prontinho! Com isso matamos a questão 😊