P2 de Física 2 da UNICAMP - 2010.1(Noturno)

Um bloco de massa , em repouso numa mesa horizontal sem atrito, é ligado a um suporte rígido por duas molas de constante elástica e . Uma bala de massa e velocidade atinge o bloco como mostrado na figura abaixo.

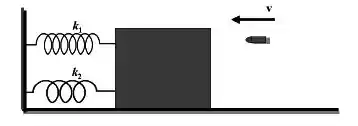
Este sistema de duas molas da figura acima é equivalente a um sistema composto por apenas uma mola cuja constante elástica vale:

1. Deduza a expressão .

Considere e determine em função de , , e :

2. A velocidade do bloco imediatamente após a colisão.
3. A amplitude do movimento harmônico simples.

Um menino está sentado próximo à janela aberta de um trem que está se movendo a uma velocidade de para o leste. O tio do menino está de pé próximo aos trilhos e vê o trem se afastar. O apito da locomotiva emite som na frequência de . O ar está parado.

Velocidade do som: .

1. Que frequência o tio ouve?
2. Que frequência o menino ouve?

Suponha agora que um vento começa a soprar vindo do leste a .

3. Que frequência o menino ouve agora?
4. Que frequência o som do apito do trem deveria ter para que o tio percebesse uma frequência aparente de ?

Um microfone é colocado no meio da linha que une dois alto-falantes de que podem ser considerados fontes pontuais isotrópicas. Os dois alto-falantes estão separados de uma distância de e emitem uma onda sonora em fase numa frequência de . Despreze as ondas sonoras refletidas na montagem. Dados:

1. Calcule o nível sonoro em medido pelo microfone se apenas um alto-falante estiver ligado.
2. Calcule a intensidade do som em se os dois alto-falantes estiverem ligados.
3. Qual a menor distância que podemos mover o microfone ao longo da linha que une os alto-falantes de modo que a intensidade sonora detectada se torne mínima.

Um tubo , que possui de comprimento e é aberto em suas duas extremidades, vibra na sua terceira frequência harmônica mais baixa. Outro tubo , de comprimento , é fechado em uma de suas extremidades e vibra em sua segunda frequência harmônica mais baixa. As frequências dos tubos e coincidem. Dado:

1. Encontre as posições do tubo em que estão os nós de deslocamento.
2. Encontre o comprimento do tubo .