Um microfone é colocado no meio da linha que une dois alto-falantes de que podem ser considerados fontes pontuais isotrópicas. Os dois alto-falantes estão separados de uma distância de e emitem uma onda sonora em fase numa frequência de . Despreze as ondas sonoras refletidas na montagem. Dados:
- Calcule o nível sonoro em medido pelo microfone se apenas um alto-falante estiver ligado.
- Calcule a intensidade do som em se os dois alto-falantes estiverem ligados.
- Qual a menor distância que podemos mover o microfone ao longo da linha que une os alto-falantes de modo que a intensidade sonora detectada se torne mínima.
Passo 1
a):
Bom, pra gente calcular o nível sonoro de apenas um alto-falante, basta que a gente calcule a intensidade do som no ponto onde está o ouvinte, no caso, no meio da linha que liga os dois alto-falantes, e após isso calcule o nível sonoro em si.
Sendo a potência do Alto-falante: , a intensidade do som na distância é:
Logo, o nível sonoro será:
Passo 2
b):
Agora a situação é outra: Os dois alto-falantes estão ligados. Precisamos achar uma expressão que nos dê a intensidade da onda sonora resultante no meio da linha que liga os dois.
Como vamos fazer isso? Bom, vamos precisar lembrar de duas fórmulas:
A segunda equação nos dá a amplitude resultante da combinação de duas ondas com fases e .
Vamos isolar e na primeira expressão e substituir na segunda:
Logo:
Eita! Vamos arrumar isso ai:
Simplificando:
Show!
Como as ondas estão em fase: .Além disso:
Logo:
Ótimo! Agora basta a gente calcular o nível sonoro dessa intensidade:
Passo 3
c):
Vamos dar uma olhada na linda figura que exemplifica a situação desse item:
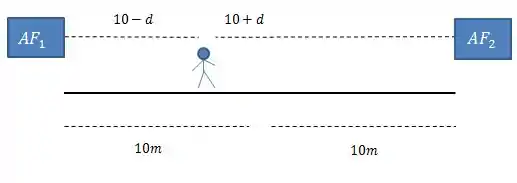
Nós queremos descobrir a menor distância tal que o observador que estava em no meio da linha que liga os dois alto-falantes pode se deslocar de forma que a intensidade do som percebida por ele seja mínima.
Isso quer dizer, como podemos ver na figura, que as distâncias dele até os alto-falantes vão ficar alteradas e passarão a ser:
Ótimo! Agora queremos descobrir quem é esse Para isso vamos usar a fórmula da interferência para o caso destrutivo:
Bom, pode ser calculado por:
Além disso, como queremos a menor distância, vamos pegar a menor diferença de fase: Quando
Obs: Isso sempre acontece! Quando queremos a menor distância, ou o menor , usamos a menor diferença de fase!
Substituindo esses valores na primeira equação:
Mas quem é ?
Vamos achar usando aquela fórmula clássica:
Substituindo na equação de
Resposta
a):
b):
c):