Listas de Física 2 - UNICAMP de Física 2 da UNICAMP - Lista 1 - Gravitação

Como mostra a figura , duas esferas de massa e uma terceira esfera de massa formam um triângulo equilátero e uma quarta esfera de massa ocupa o centro do triângulo. A força gravitacional sobre a esfera central é nula.

Qual é o valor de em termos de ?

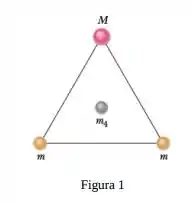
Como mostra a figura , duas esferas de massa e uma terceira esfera de massa formam um triângulo equilátero e uma quarta esfera de massa ocupa o centro do triângulo. A força gravitacional sobre a esfera central é nula.

Se dobrarmos o valor de , qual será o novo módulo da força gravitacional a que está submetida a esfera central?

Três estrelas, cada uma com a massa do Sol, formam um triângulo equilátero com lados de . (Este triângulo se encaixaria com precisão da órbita de Júpiter). O triângulo precisa girar, pois do contrário, as estrelas colidiram no centro. Qual é o período de rotação? Expresse sua resposta em anos.

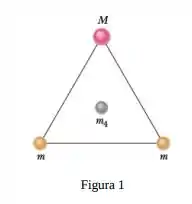
A figura mostra uma cavidade esférica no interior de uma esfera de chumbo de raio ; a superfície da cavidade passa pelo centro da esfera e “toca” o lado direito da esfera. A massa da esfera antes de ser criada a cavidade era . Com que força gravitacional a esfera de chumbo com a cavidade atrai uma pequena esfera de massa que se encontra a uma distância do centro da esfera de chumbo, sobre a reta que liga os centros das esferas e o centro da cavidade?

Acredita-se que alguma estrelas de nêutrons (estrelas extremamente densas) estão girando a cerca de . Se uma dessas estrelas têm um raio de , qual deve ser, no mínimo, a sua massa para que uma partícula na superfície da estrela permaneça no lugar apesar da rotação?

Suponha que um planeta é uma esfera homogênea de raio que (de alguma forma) possui um túnel radial estreito que passa pelo centro do planeta (figura 3). Suponha também que é possível posicionar uma maçã em qualquer lugar do túnel ou do lado de fora do planeta. Seja o módulo da força gravitacional experimentada pela maçã quando está na superfície do planeta. A que distância da superfície está o ponto no qual o módulo da força gravitacional que o planeta exerce sobre a maçã é se a maçã for deslocada:

Para longe do planeta?

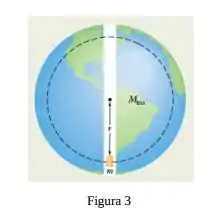
Suponha que um planeta é uma esfera homogênea de raio que (de alguma forma) possui um túnel radial estreito que passa pelo centro do planeta (figura 3). Suponha também que é possível posicionar uma maçã em qualquer lugar do túnel ou do lado de fora do planeta. Seja o módulo da força gravitacional experimentada pela maçã quando está na superfície do planeta. A que distância da superfície está o ponto no qual o módulo da força gravitacional que o planeta exerce sobre a maçã é se a maçã for deslocada:

Para dentro do túnel?

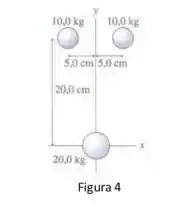
Qual é o módulo e qual é a direção da força gravitacional resultante sobre a massa de da figura ?

Suponha que a Terra de repente parasse de girar em torno do Sol. A força gravitacional a atrairia diretamente para o Sol. Qual seria a velocidade da Terra quando colidisse com ele?

Plutão se movimenta em uma órbita claramente elíptica em torno do Sol. A velocidade de Plutão em seu ponto mais próximo, do Sol é de . Qual é a velocidade de Plutão no ponto mais distante de sua órbita, onde se encontra a do Sol?

Duas estrelas de nêutrons estão separadas por uma distância de . Ambas tem uma massa de e um raio de . As estrelas se encontram inicialmente em repouso relativo. Com que velocidade estarão se movendo, em relação a este referencial de repouso:

Quando a distância for metade do valor inicial?

Duas estrelas de nêutrons estão separadas por uma distância de . Ambas tem uma massa de e um raio de . As estrelas se encontram inicialmente em repouso relativo. Com que velocidade estarão se movendo, em relação a este referencial de repouso:

Quando estiverem na iminência de colidir?

Um satélite está em órbita circular de raio em torno da Terra. A área delimitada pela órbita é proporcional a , já que . Determine a forma de variação com das seguintes propriedades do satélite:

O período;

Um satélite está em órbita circular de raio em torno da Terra. A área delimitada pela órbita é proporcional a , já que . Determine a forma de variação com das seguintes propriedades do satélite:

A energia cinética;

Um satélite está em órbita circular de raio em torno da Terra. A área delimitada pela órbita é proporcional a , já que . Determine a forma de variação com das seguintes propriedades do satélite:

O momento angular;

Um satélite está em órbita circular de raio em torno da Terra. A área delimitada pela órbita é proporcional a , já que . Determine a forma de variação com das seguintes propriedades do satélite:

A velocidade escalar.