P2 de Física 2 da UNICAMP - 2012.1(Diurno)

Uma corda presa a um oscilador senoidal no ponto e apoiada em um suporte no ponto (vide figura), é tensionada por um bloco de massa . A distância entre e é , a massa específica linear da corda é e a frequência do oscilador é . A amplitude de deslocamento do ponto é suficientemente pequena para que esse ponto seja considerado um nó. Também existe um nó no ponto .

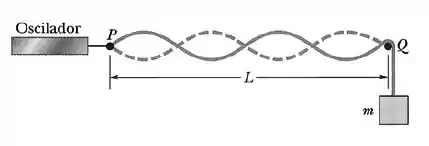
1. Qual deve ser o valor da massa para que o oscilador produza na corda o quarto harmônico?
2. Se , qual é a frequência do quarto harmônico?

Se necessário, use .

Um bloco de massa desliza sem atrito sobre um plano inclinado que faz um ângulo com a horizontal e tem uma mola fixa no final da rampa. O bloco é solto de uma posição inicial tal que a distância entre a ponta livre da mola e a face do bloco é . Quando o bloco bate na mola, um dispositivo é acionado conectando o bloco na mola. O bloco comprime a mola até um valor máximo igual a , quando a velocidade instantânea do bloco torna-se zero. Considere um eixo ao longo do plano inclinado no sentido descendente e com sua origem na posição da ponta livre da mola quando ela não está deformada. Determine, em função dos parâmetros fornecidos e da aceleração da gravidade no local:

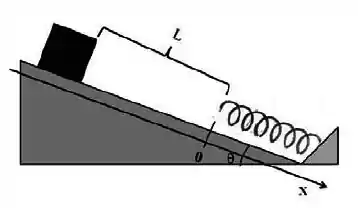
1. A frequência angular do movimento harmônico simples que o bloco executa após conectar-se à mola.
2. A posição na qual a velocidade do bloco é máxima.
3. A posição mais alta que o bloco alcança após conectar-se à mola.

Uma onda estacionária é produzida num tubo de de comprimento, aberto em uma extremidade e fechado na outra. Um detector afasta-se do tubo em line reta, e capta parte da onda sonora que escapa do tubo.

1. Se a onda estacionária corresponde ao terceiro harmônico do tubo, qual deve ser a velocidade do detector para que a frequência detectada corresponda à frequência fundamental do tubo?
2. Considere agora que o mesmo tubo seja aberto nas duas extremidades e que novamente a onda estacionária corresponda ao terceiro harmônico. Qual deve ser a velocidade do detector neste caso para que a frequência detectada corresponda à frequência fundamental do tubo?

Dado:

Use para a velocidade do som no ar.

Uma onda sonora com comprimento de onda de propaga-se para a direita num tubo que possui uma bifurcação (vide figura). Ao chegar à bifurcação a onda se divide em duas partes. Uma propaga-se em um tubo em forma de semicircunferência, e a outra se propaga em um tubo retilíneo. As duas ondas combinam-se mais adiante, antes de chegarem ao detector. Qual é o menor raio da semicircunferência para o qual a intensidade medida pelo detector é mínima? Se necessário, use .