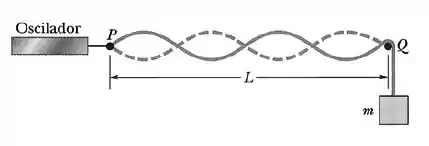
Uma corda presa a um oscilador senoidal no ponto e apoiada em um suporte no ponto (vide figura), é tensionada por um bloco de massa . A distância entre e é , a massa específica linear da corda é e a frequência do oscilador é . A amplitude de deslocamento do ponto é suficientemente pequena para que esse ponto seja considerado um nó. Também existe um nó no ponto .
- Qual deve ser o valor da massa para que o oscilador produza na corda o quarto harmônico?
- Se , qual é a frequência do quarto harmônico?
Se necessário, use .
Passo 1
a):
Bom galera, a frequência da corda é dada pela fórmula:
A velocidade de propagação da onda que aparece na fórmula pode ser calculada por:
A gente sabe , mas quem é ?
A tensão vai ser dada pelo peso da massinha:
Logo:
Se liga na mudança feita ali: .
Passo 2
Vamos continuar resolvendo a primeira opção:
Agora sabemos o valor de em função de . Vamos jogar na fórmula:
Bem:
Logo:
Passo 3
b):
Bom, se massa for , a tensão vai mudar e, consequentemente, a velocidade de propagação também. Logo, a frequência do quarto harmônico também mudará:
Logo:
Resposta
a):
b):