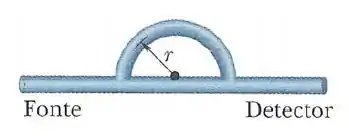
Uma onda sonora com comprimento de onda de propaga-se para a direita num tubo que possui uma bifurcação (vide figura). Ao chegar à bifurcação a onda se divide em duas partes. Uma propaga-se em um tubo em forma de semicircunferência, e a outra se propaga em um tubo retilíneo. As duas ondas combinam-se mais adiante, antes de chegarem ao detector. Qual é o menor raio da semicircunferência para o qual a intensidade medida pelo detector é mínima? Se necessário, use .
Passo 1
Bom galera, vamos primeiro identificar do que se trata o problema:
Bem, como queremos saber uma condição para que a intensidade da combinação de duas frentes de ondas seja mínima, estamos lidando com interferência.
E qual o tipo de interferência que o enunciado pede? Como ele quer uma intensidade resultante mínima, a interferência só pode ser destrutiva, afinal, numa interferência construtiva a intensidade das frentes de onda é máxima, já que elas se somam.
Pela nossa teoria, a equação que vamos usar é:
Onde:
Ou seja, a fase é um múltiplo ímpar de .
Passo 2
Vamos por a mão na massa:
Bom, a onda se divide em duas: Uma que segue pela semicircunferência e outra que vai pela parte de baixo da mesma.
O comprimento da semicircunferência é a metade do que teria o círculo de raio , ou seja:
Já embaixo, a onda percorre um caminho que equivale a :
Logo:
Pra usar a equação que vimos ali encima basta saber o valor do comprimento da onda.Opa!Ele já disse isso: . Logo:
Passo 3
Vamos analisar o resultado agora:
Para que a interferência seja destrutiva, é preciso que a diferença de fase seja um múltiplo ímpar de e, além disso, como queremos o menor raio que gere esse efeito, precisamos, também, do menor múltiplo ímpar de
Quem é o menor múltiplo de Ora, o próprio
Logo:
Pronto (: