Um bloco de massa desliza sem atrito sobre um plano inclinado que faz um ângulo com a horizontal e tem uma mola fixa no final da rampa. O bloco é solto de uma posição inicial tal que a distância entre a ponta livre da mola e a face do bloco é . Quando o bloco bate na mola, um dispositivo é acionado conectando o bloco na mola. O bloco comprime a mola até um valor máximo igual a , quando a velocidade instantânea do bloco torna-se zero. Considere um eixo ao longo do plano inclinado no sentido descendente e com sua origem na posição da ponta livre da mola quando ela não está deformada. Determine, em função dos parâmetros fornecidos e da aceleração da gravidade no local:
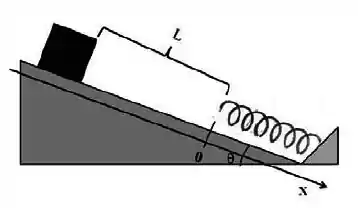
- A frequência angular do movimento harmônico simples que o bloco executa após conectar-se à mola.
- A posição na qual a velocidade do bloco é máxima.
- A posição mais alta que o bloco alcança após conectar-se à mola.
Passo 1
Vamos, primeiramente, escrever a equação diferencial associada ao bloco:
Bom, quais são as forças que atuam sobre o bloco?
As forças que atuam sobre o bloco são a força peso e a força elástica.
Então, pela segunda lei de Newton:
No entanto, como estamos lidando com um plano inclinado, a força peso terá apenas uma componente (lembra disso em mecânica?(: ):
E a força elástica é:
Logo, agora se importando apenas com os módulos:
Sendo :
Passo 2
a):
Aqui a questão pede a frequência angular. A gente sabe que a frequência angular aparece, elevado ao quadrado, na nossa EDO como o termo que acompanha o :
Logo:
Só que a gente não sabe quem é ! Não foi dado no problema. HUUM, vamos ter que pensar um pouco aqui.
Bem, o enunciado diz que o bloco estava afastado por uma distância da origem estabelecida na figura, e que, depois que ele toca na mola, o mesmo ainda se afasta na direção negativa de .
Por isso a gente pode montar a figura:
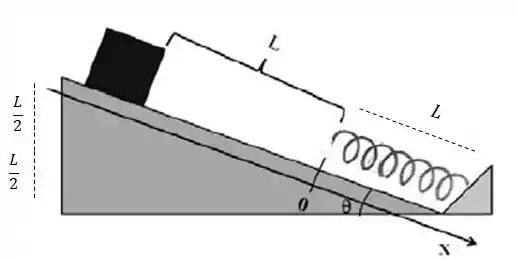
O valor do cateto do triangulo é esse graças ao valor de . Logo, sabemos que o o bloco saiu de uma para uma altura zero. Então vamos aplicar a conservação da energia:
No início havia apenas energia potencial gravitacional, e no fim passou a ter apenas energia potencial elástica, ou seja:
Logo:
Passo 3
b):
Bem, após a conexão com a mola, o bloco vai passar a oscilar em torno do ponto determinado pela figura da questão com uma amplitude .
Quando o bloco atinge os seus extremos de oscilação, ou , a sua velocidade é zero, pelo que sabemos do estudo dos MHS, logo, nesses pontos, a energia é toda potencial elástica.
E quando ele passa pelo ponto , como não há deslocamento , a sua velocidade é máxima, pois nesse caso a energia é toda cinética.
Logo, o ponto para o qual a velocidade é máxima é o ponto
Passo 4
c):
Aqui a gente pode fazer de uma forma muito simples, usando de nova a conservação da energia. Quando o bloco está na posição mais baixa, com a altura vertical , a sua energia é toda elástica. Como a energia se conserva, quando ele estiver na altura máxima, a mesma valerá:
Onde vai ser o valor da elongação. Logo, a energia no segundo instante será a soma da energia potencial gravitacional mais a energia potencial da mola. Por conservação da energia mecânica:
Resolvendo a equação em e lembrando do valor de :
Logo, a altura máxima é:
Resposta
a):
b):
c):