P2 de Física 3 da UNICAMP - 2011.2 - Diurno

Um fio, transportando uma corrente , é dobrado de modo a formar uma espira semicircular de raio , conforme a figura. O fio está no plano e o vetor é dado por .

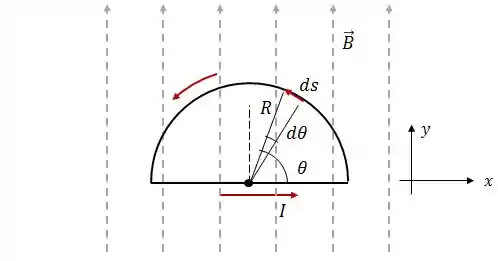
Calcule a força magnética que age sobre a parte reta do fio;

Calcule a força magnética que age sobre a parte curva do fio;

Calcule a força magnética que age sobre a espira;

Calcule o vetor momento de dipolo magnético da espira;

Calcule o torque magnético sobre a espira;

Um condutor coaxial de comprimento , mostrado abaixo é formado por um núcleo metálico cilíndrico de raio , e resistividade , colocado no interior de uma casca metálica cilíndrica e maciça, de raio interno , raio externo e resistividade .

O cilindro e a casca estão eletricamente isolados devido à colocação, entre os mesmos, de um filme isolante de espessura desprezível. O condutor coaxial é então ligado a um circuito, conectando-se firmemente toda a área de suas extremidades planas com o uso de placas metálicas de resistência elétrica desprezível.

A densidade de corrente que circula pelo condutor coaxial é dada por , para , , para .

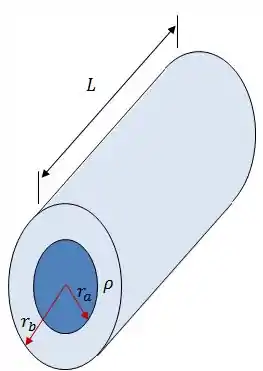
Calcular para o condutor coaxial:

A corrente total que o atravessa.

Sua resistência equivalente.

A d.d.p. entre duas extremidades.

Três capacitores de placas planas e paralelas estão ligados como mostra a figura abaixo. Inicialmente, os capacitores e estão descarregados e está carregado com carga . A chave é então fechada.

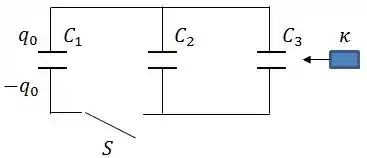
Calcular a carga em cada capacitor e a diferença de potencial através dos mesmos após o estabelecimento do equilíbrio.

Mantendo-se a chave fechada é inserido um material de constante dielétrica no capacitor , preenchendo totalmente o volume entre suas placas.

Nesta nova situação, calcular a carga em cada capacitor e a diferença de potencial através dos mesmos, após o restabelecimento do equilíbrio.

Calcular a variação da energia potencial elétrica em , onde é a energia antes do fechamento da chave e é a energia após a colocação do dielétrico.

No circuito abaixo, no instante (chave aberta).

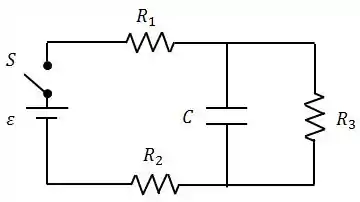
O capacitor encontra-se descarregado. Considerando que a bateria que alimenta o circuito é ideal e com força eletromotriz , calcule, após o fechamento da chave :

A corrente que atravessa o capacitor, imediatamente após o fechamento de ;

A corrente que passa pelo resistor , imediatamente após o fechamento de ;

A corrente que atravessa pela chave e a carga no capacitor em ;

A carga do capacitor e a corrente que atravessa os resistores e em função do tempo;