Um fio, transportando uma corrente , é dobrado de modo a formar uma espira semicircular de raio , conforme a figura. O fio está no plano e o vetor é dado por .
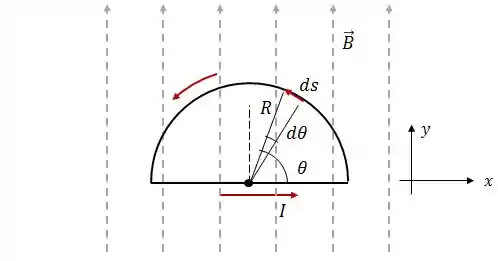
Calcule a força magnética que age sobre a parte reta do fio;
Calcule a força magnética que age sobre a parte curva do fio;
Calcule a força magnética que age sobre a espira;
Calcule o vetor momento de dipolo magnético da espira;
Calcule o torque magnético sobre a espira;
Passo 1
Calcule a força magnética que age sobre a parte reta do fio;
A força magnética sobre um condutor é dada por:
Onde é um pedaço infinitesimal do condutor, cujo vetor tem a mesma direção e sentido da corrente.
No caso de um condutor retilíneo, podemos dar uma simplificada nesse cara, que passará a ser dado por:
Onde também tem a mesma direção e sentido da corrente.
Nesse caso:
Portanto:
Finalmente:
Passo 2
Calcule a força magnética que age sobre a parte curva do fio;
Nesse caso, será um pedaço infinitesimal da circunferência.
Onde , logo:
Onde . Assim, substituindo esses dados na expressão de , teremos:
Passo 3
Calcule a força magnética que age sobre a espira;
A força magnética sobre a espira será a soma das forças magnéticas sobre o segmento retilíneo e o segmento curvo.
Passo 4
Calcule o vetor momento de dipolo magnético da espira;
Por definição, o momento de dipolo magnético é dado por:
Onde tem módulo igual à área da espira. A direção e o sentido são determinados com a regra da mão direita, usando o sentido da corrente na espira como base.
Nesse caso, como a corrente está no sentido anti-horário:
Portanto:
Passo 5
Calcule o torque magnético sobre a espira;
O torque magnético sobre uma espira é dado por:
Substituindo e , teremos:
Finalmente:
Resposta