No circuito abaixo, no instante (chave aberta).
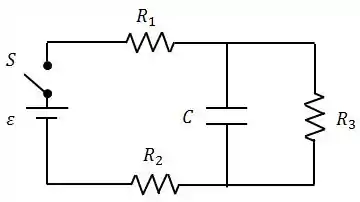
O capacitor encontra-se descarregado. Considerando que a bateria que alimenta o circuito é ideal e com força eletromotriz , calcule, após o fechamento da chave :
A corrente que atravessa o capacitor, imediatamente após o fechamento de ;
A corrente que passa pelo resistor , imediatamente após o fechamento de ;
A corrente que atravessa pela chave e a carga no capacitor em ;
A carga do capacitor e a corrente que atravessa os resistores e em função do tempo;
Passo 1
A corrente que atravessa o capacitor, imediatamente após o fechamento de ;
Imediatamente após o fechamento de , a carga no capacitor ainda é nula, logo, a diferença de potencial entre os terminais do capacitor também será nula.
Basicamente, o que vai acontecer é que a corrente vai sair da fonte, passar pelo resistor e a corrente vai toda para o capacitor (onde não há diferença de potencial), seguindo para antes de retornar à fonte.
Essa corrente é dada por:
Passo 2
A corrente que passa pelo resistor , imediatamente após o fechamento de ;
Conforme discutimos na letra , como a diferença de potencial no capacitor imediatamente após o fechamento de é nula, nesse instante, toda a corrente flui para o capacitor.
Assim, a corrente que passa por imediatamente, após o fechamento de , é nula.
Passo 3
A corrente que atravessa pela chave e a carga no capacitor em ;
Em , o capacitor está completamente carregado, não passando mais nenhuma corrente pode ele. Assim, toda a corrente agora vai para o resistor .
Portanto, a corrente, agora, no circuito será:
Nesse momento, a diferença de potencial no capacitor será, de acordo com a Lei das malhas:
Onde . Logo:
Passo 4
A carga do capacitor e a corrente que atravessa os resistores e em função do tempo;
De acordo com a Lei das malhas de Kirchhoff, percorrendo a malha que possui a fonte , os resistores e e o capacitor , teremos:
Percorrendo a malha que possui o capacitor e o resistor , teremos:
De acordo com a Lei dos nós de Kirchhoff, teremos:
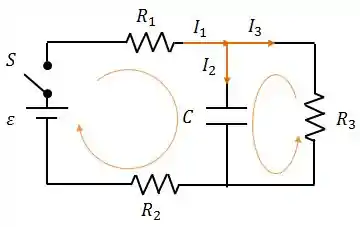
Ok... voltando para a primeira equação, podemos reescrevê-la como:
Substituindo pelo que encontramos pela lei das malhas:
Vamos dar uma ajeitada nesse cara:
nesse caso é a corrente que atravessa o capacitor.
A equação acima nos leva a uma equação diferencial, já que .
O próximo passo agora é resolver a equação diferencial.
Passo 5
Pra começar, vamos dar uma simplificada nesse cara, vamos chamar de e os seguintes caras:
Assim:
Melhorou bastante. Bom, essa é uma equação separável, então vamos lá:
Substituindo de volta as expressões de e , teremos:
Arrumando esse cara, finamente, teremos:
Agora temos que determinar a corrente nos resistores e em função do tempo.
Passo 6
A corrente que passa pelos resistores e é a corrente . De acordo com a Lei dos nós:
Então o nosso trabalho aqui é determinar e .
A corrente é dada por:
Simplificando esse cara, teremos:
A corrente é dada por:
Substituindo a expressão de , teremos:
Simplificando esse cara:
Finalmente:
Resposta