Três capacitores de placas planas e paralelas estão ligados como mostra a figura abaixo. Inicialmente, os capacitores e estão descarregados e está carregado com carga . A chave é então fechada.
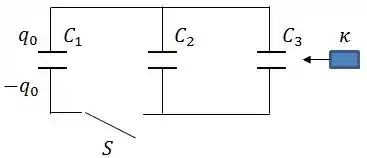
Calcular a carga em cada capacitor e a diferença de potencial através dos mesmos após o estabelecimento do equilíbrio.
Mantendo-se a chave fechada é inserido um material de constante dielétrica no capacitor , preenchendo totalmente o volume entre suas placas.
Nesta nova situação, calcular a carga em cada capacitor e a diferença de potencial através dos mesmos, após o restabelecimento do equilíbrio.
Calcular a variação da energia potencial elétrica em , onde é a energia antes do fechamento da chave e é a energia após a colocação do dielétrico.
Passo 1
Calcular a carga em cada capacitor e a diferença de potencial através dos mesmos após o estabelecimento do equilíbrio.
Após o estabelecimento do equilíbrio, duas coisas devem acontecer:
- Os três capacitores deve apresentar a mesma diferença de potencial ;
- A soma das cargas dos três capacitores deve ser igual a ;
Logo:
As cargas de cada capacitor serão dadas por:
Passo 2
Somando as três cargas:
Finalmente:
E as cargas em cada capacitor serão:
Passo 3
Nesta nova situação, calcular a carga em cada capacitor e a diferença de potencial através dos mesmos, após o restabelecimento do equilíbrio.
Assim que adicionamos o dielétrico no capacitor , as capacitâncias passarão a ser:
Como os três capacitores continuam em paralelo, eles devem ter a mesma diferença de potencial . Além disso, a somas das cargas deve continuar sendo igual a .
Então a ideia aqui é a mesma que usamos anteriormente.
Somando as cargas, teremos:
Finalmente:
E as cargas será dadas por:
Passo 4
Calcular a variação da energia potencial elétrica em , onde é a energia antes do fechamento da chave e é a energia após a colocação do dielétrico.
A energia potencial elétrica armazenada em um capacitor é dada por:
Logo, a energia inicial no capacitor 1 é dada por:
E a energia final no capacitor 1 é dada por:
Como no passo anterior já calculamos a carga final
Portanto:
Resposta