Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Resistencia em Série e em Paralelo

Ver Teoria
Exercício 151234567891011121314161718192021222324

Enunciado

Corrente e Resistores, Circuitos

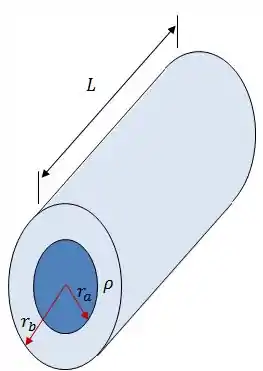
Um condutor coaxial de comprimento L , mostrado abaixo é formado por um núcleo metálico cilíndrico de raio r a , e resistividade ρ / 3 , colocado no interior de uma casca metálica cilíndrica e maciça, de raio interno r a , raio externo r b e resistividade ρ .

O cilindro e a casca estão eletricamente isolados devido à colocação, entre os mesmos, de um filme isolante de espessura desprezível. O condutor coaxial é então ligado a um circuito, conectando-se firmemente toda a área de suas extremidades planas com o uso de placas metálicas de resistência elétrica desprezível.

A densidade de corrente que circula pelo condutor coaxial é dada por J → = 3 J 0 k ^ , para r < r a , J → = J 0 k ^ , para r a < r < r b .

Calcular para o condutor coaxial:

a ) A corrente total que o atravessa.

b ) Sua resistência equivalente.

c ) A d.d.p. entre duas extremidades.

Passo 1

a ) A corrente total que o atravessa.

O problema deu apenas as densidades de corrente do cilindro interno e da casca cilíndrica.

Pode definição, a corrente será dada por:

I = ∬ S J → ∙ d A →

Assim, a corrente total será a soma das correntes que passam pelo cilindro e pela casca cilíndrica.

  • Cilindro:

    • J → = 3 J 0 k ^

    Logo:

    I c i l = ∬ S 3 J 0   d A = 3 J 0 ∬ S d A

    I c i l = 3 J 0 A

    Onde A é a área da seção transversal do cilindro, dada por A = π r a 2 . Logo:

    I c i l = 3 J 0 π r a 2

  • Casca cilíndrica:

    • J → = J 0 k ^

    I c a s c a = ∬ S J 0   d A = J 0 ∬ S d A = J 0 A

    Novamente, A será a área da seção transversal da casca cilíndrica que, nesse caso, é a coroa circular. Sendo assim, A = π r b 2 - r a 2 :

    I c a s c a = J 0 π r b 2 - r a 2

    Finalmente:

    I = I c i l + I c a s c a

    I = 3 J 0 π r a 2 + J 0 π r b 2 - r a 2

    I = 2 J 0 π r a 2 + J 0 π r b 2

    I = J 0 π 2 r a 2 + r b 2

    Passo 2

    b ) Sua resistência equivalente.

    Por definição, a resistência é dada por:

    R = ρ L A

    Vamos começar calculando a resistência de cada elemento.

  • Cilindro:

    • R c i l = ρ L 3 π r a 2

  • Casca cilíndrica:

R c a s c a = ρ L π r b 2 - r a 2

Pra calcularmos a resistência equivalente, vamos pensar no seguinte: uma corrente que percorre o condutor vai passar ou pelo cilindro, ou pela casca cilíndrica, concorda?

Isso significa que podemos pensar nesses dois caras como sendo resistores em paralelo. Nesse caso, a resistência equivalente será dada por:

1 R e q = 1 R c i l + 1 R c a s c a

R e q = R c i l . R c a s c a R c i l + R c a s c a

Substituindo as expressões que encontramos aqui em cima:

R e q = ρ L 3 π r a 2 . ρ L π r b 2 - r a 2 ρ L 3 π r a 2 + ρ L π r b 2 - r a 2

Agora o nosso trabalho é dar uma simplificada nesse cara:

R e q = ρ 2 L 2 3 π 2 r a 2 r b 2 - r a 2 ρ L π 1 3 r a 2 + 1 r b 2 - r a 2

R e q = ρ L 3 π r a 2 r b 2 - r a 2 1 3 r a 2 + 1 r b 2 - r a 2

R e q = ρ L 3 π r a 2 r b 2 - r a 2 2 r a 2 + r b 2 3 r a 2 r b 2 - r a 2 = ρ L 3 π r a 2 r b 2 - r a 2 3 r a 2 r b 2 - r a 2 2 r a 2 + r b 2

Finalmente:

R e q = ρ L π 2 r a 2 + r b 2

Passo 2

c ) A d.d.p. entre duas extremidades.

Bom, já calculamos a corrente total e a resistência equivalente... então, para achar a d.d.p., bastar usar a Lei de Ohm:

V = R I

No caso:

V = R e q I

Substituindo o que encontramos nas letras a e b , teremos:

V = ρ L π 2 r a 2 + r b 2   J 0 π 2 r a 2 + r b 2

Simplificando, teremos:

V = ρ L J 0

Resposta

a )

I = J 0 π 2 r a 2 + r b 2

b )

R e q = ρ L π 2 r a 2 + r b 2

c )

V = ρ L J 0

Exercícios de Livros Relacionados

71- Um resistor R 1 consome uma energia elétrica P 1 , quando conectada a uma f e mϵ . Quando o resistor R 2 é conectado a mesma f e m , ela consome energia elétrica P 2 . Em termos de P 1 e P 2 , qua
Uma combinação em paralelo dos resistores A e B está conectada aos terminais de uma bateria. O resistor A tem o dobro da resistência do resistor B . Se a corrente conduzida pelo resistor A é I , então
Na Fig. 27-82, uma fonte ideal de força eletromotriz ε =12,0V é ligada a um circuito cujasresistências s ã oR 1=6,00Ω ,R 2=12,00Ω ,R 3=4,00Ω ,R 4=3,00ΩeR 5=5,00Ω ã . Qual é a diferença de potencial da
Uma lâmpada de120V com dois filamentos pode operar em três níveis de potência: 100 ,200 e300W . Um dos filamentos queima. Depois disso, a lâmpada funciona com a mesma luminosidade (dissipa a mesma pot
Um equipamento possui um resistor X que se projeta de uma abertura lateral. Esse resistor é conectado a outros três resistores, como indica a Figura 26.38. Um ohmímetro conectado através de a e b regi