P2 de Física III da UFF - 2015.1

Uma maquina térmica:

1. Converte calor de entrada em uma quantidade equivalente de trabalho.
2. Converte trabalho em uma quantidade equivalente de calor.
3. Recebe calor, realiza trabalho, e perde calor.
4. Utiliza trabalho para transferir calor de um reservatório a baixa temperatura para outro reservatório a alta temperatura.
5. Em um ciclo produz trabalho equivalente ao calor rejeitado ao reservatório frio.

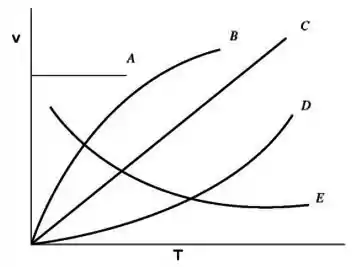
Considere pontos no diagrama com as seguintes pressões e volumes. Ponto A:

(2,); Ponto B: (,2); Ponto C: (,2); Ponto D: (,). Considere que de um gás ideal sejam colocados para realizar os seguintes ciclos:

Ciclo : o gás passa por uma expansão isobárica do ponto A até o ponto B, e depois por um processo isocórico do ponto B para o ponto C. Em seguida, é comprimido isobaricamente do ponto C para o ponto D e finalmente retorna isocoricamente ao ponto A.

Ciclo : o gás passa por uma expansão isobárica do ponto A ate o ponto B, e depois por um processo isocórico do ponto B para o ponto C. Finalmente, o gás é comprimido isotermicamente do ponto C para o ponto A.

Ainda com relação aos ciclos, assinale a opção CORRETA:

1. No ciclo , o calor trocado no trecho é positivo.
2. No ciclo , o calor trocado no trecho é negativo.
3. No ciclo , a variação de energia térmica no trecho é negativa.
4. No ciclo , o trabalho realizado pelo sistema no trecho é negativo e no trecho é positivo.
5. No ciclo , a energia termica diminui no trecho .

Dois alto-falantes A e B estão localizados no eixo como mostra a figura abaixo. Eles estão separados por uma distancia de . Cada alto-falante emite ondas sonoras em sentidos opostos, A no sentido e B no sentido , com frequências iguais a , e as fontes estão fora de fase em . A velocidade do som e . A que distancia do alto-falante A ocorrerá o primeiro ponto de interferência construtiva?

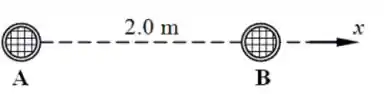
Considere pontos no diagrama com as seguintes pressões e volumes. Ponto A:

(2,); Ponto B: (,2); Ponto C: (,2); Ponto D: (,). Considere que de um gás ideal sejam colocados para realizar os seguintes ciclos:

Ciclo : o gás passa por uma expansão isobárica do ponto A até o ponto B e depois por um processo isocórico do ponto B para o ponto C. Em seguida, é comprimido isobaricamente do ponto C para o ponto D e finalmente retorna isocoricamente ao ponto A.

Ciclo : o gás passa por uma expansão isobárica do ponto A até o ponto B, e depois por um processo isocórico do ponto B para o ponto C. Finalmente, o gás e comprimido isotermicamente do ponto C para o ponto A.

Com relação a estes dois ciclos e , podemos afirmar que:

1. Ambos podem representar o funcionamento de uma maquina térmica.
2. Ambos podem representar o funcionamento de um refrigerador.
3. O ciclo pode representar uma maquina termica e o ciclo um refrigerador.
4. O ciclo pode representar um refrigerador e o ciclo uma maquina térmica.
5. No ciclo seria possivel trocar o processo isotérmico por um processo adiabático.

Considere pontos no diagrama com as seguintes pressões e volumes. Ponto A:

(2,); Ponto B: (,2); Ponto C: (,2); Ponto D: (,). Considere que de um gás ideal sejam colocados para realizar os seguintes ciclos:

Ciclo : o gás passa por uma expansão isobárica do ponto A até o ponto B, e depois por um processo isocórico do ponto B para o ponto C. Em seguida, é comprimido isobaricamente do ponto C para o ponto D e finalmente retorna isocoricamente ao ponto A.

Ciclo : o gás passa por uma expansão isobárica do ponto A ate o ponto B, e depois por um processo isocórico do ponto B para o ponto C. Finalmente, o gás é comprimido isotermicamente do ponto C para o ponto A.

Ainda considerando os ciclos e , assinale a opção CORRETA:

1. O rendimento tanto do ciclo quanto do ciclo depende do numero de mols n do gás.
2. O rendimento tanto o ciclo quanto do ciclo não dependem do tipo de gás (monoatômico ou diatômico).
3. O rendimento tanto o ciclo quanto do ciclo dependem dos valores e .
4. Independente do tipo de gás (monoatômico ou diatômico), o rendimento de e maior que a de .
5. Independente do tipo de gás (monoatômico ou diatômico), o rendimento de e menor que a de .

Um tubo aberto-fechado produz um som que tem frequência fundamental de Se você abrir a parte fechada do tubo, qual será o novo valor da frequência fundamental?

Uma corda de guitarra e fixada nas duas extremidades. Se você apertar a corda para aumentar a sua tensão

1. As frequências dos modos normais irão aumentar e os comprimentos de onda associados não serão afetados.
2. O comprimento de onda aumenta e a frequência dos modos normais não e alterada.
3. As frequências dos modos normais irão aumentar e os comprimentos de onda associados irão diminuir.
4. Ambos, comprimento de onda e frequência, irão aumentar.
5. Ambos, comprimento de onda e frequência, não serão alterados.

Em um tubo de ressonância que e aberto numa extremidade e fechado na outra extremidade, há:

1. Nodos de deslocamento em cada extremidade.
2. Antinodos de deslocamento em cada extremidade.
3. Um nodo de deslocamento na extremidade aberta e um antinodo de pressão na extremidade fechada.
4. Um antinodo de deslocamento na extremidade aberta e um nodo de pressão na extremidade fechada.
5. Um nodo de deslocamento na extremidade fechada e um nodo de pressão na extremidade aberta.

A intensidade de uma onda sonora é 100 vezes a intensidade de outra onda sonora . Com relação ao nível de intensidade, o da onda A em comparação com o da onda B é:

1. maior.
2. maior.
3. maior.
4. maior.
5. maior.

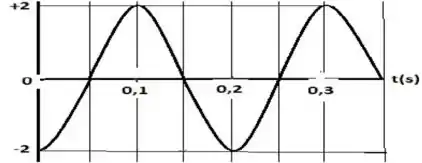
Um dado ponto em uma corda por onde passa uma onda senoidal apresenta maior velocidade quando:

1. O modulo do deslocamento é mínimo
2. O modulo do deslocamento é um quarto da amplitude.
3. O modulo da aceleração é máximo.
4. O modulo do deslocamento é máximo.
5. O modulo do deslocamento é metade da amplitude

Ondas estacionárias são produzidas pela interferência de duas ondas progressivas senoidais, cada uma com frequência . A distância do segundo nodo para o quinto nodo e de . O comprimento de onda e a velocidade das duas ondas originais são respectivamente:

Duas cordas foram amarradas uma na outra com um no e depois esticadas entre 2 suportes rígidos, conforme a figura abaixo. As cordas têm densidades lineares e . Seus comprimentos são e . A tensao e a mesma em ambas as cordas e vale . Simultaneamente, um pulso e enviado a partir da extremidade rígida de cada corda em direção ao nó. O tempo para cada pulso chegar ao nó será:

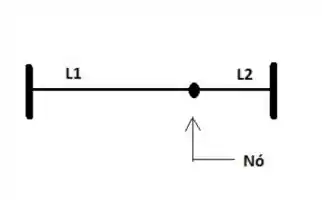
5. Não é possível determinar os tempos sem conhecer a frequência das ondas nas cordas

Na figura abaixo, qual e a curva que melhor representa o comportamento da velocidade da onda em uma corda com a tensão na corda?

1. A
2. B
3. C
4. D
5. E

O gráfico-historia de uma onda senoidal que se desloca na direção positiva do eixo a , e mostrado na figura abaixo. A equação de deslocamento dessa onda é: