Escrever a Tag aqui (nome do capítulo IGUALZINHO), Outra tag, Mais uma tag
Considere pontos no diagrama com as seguintes pressões e volumes. Ponto A:
(2,); Ponto B: (,2); Ponto C: (,2); Ponto D: (,). Considere que de um gás ideal sejam colocados para realizar os seguintes ciclos:
Ciclo : o gás passa por uma expansão isobárica do ponto A até o ponto B, e depois por um processo isocórico do ponto B para o ponto C. Em seguida, é comprimido isobaricamente do ponto C para o ponto D e finalmente retorna isocoricamente ao ponto A.
Ciclo : o gás passa por uma expansão isobárica do ponto A ate o ponto B, e depois por um processo isocórico do ponto B para o ponto C. Finalmente, o gás é comprimido isotermicamente do ponto C para o ponto A.
Ainda considerando os ciclos e , assinale a opção CORRETA:
- O rendimento tanto do ciclo quanto do ciclo depende do numero de mols n do gás.
- O rendimento tanto o ciclo quanto do ciclo não dependem do tipo de gás (monoatômico ou diatômico).
- O rendimento tanto o ciclo quanto do ciclo dependem dos valores e .
- Independente do tipo de gás (monoatômico ou diatômico), o rendimento de e maior que a de .
- Independente do tipo de gás (monoatômico ou diatômico), o rendimento de e menor que a de .
Passo 1
Vamos desenhar os dois ciclos :
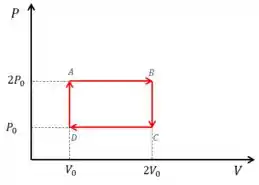
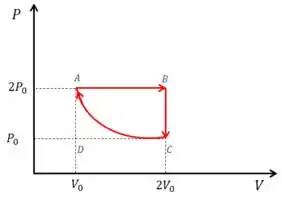
Passo 2
Ambos os ciclos representam máquinas térmicas, já que o sentido deles é positivo. A eficiência de uma máquina térmica é dada por:
Bora então calcular o trabalho e o calor absorvido em cada ciclo.
Passo 3
O calor absorvido é o mesmo para os dois ciclos e é recebido pelo sistema no trecho . Então ele é dado por:
Pra , o trabalho é dado pela soma do trabalho realizado em e o trabalho realizado em . Esse último é negativo, já que é uma compressão:
Pra , o trabalho será dado pelo trabalho de e o trabalho de , da mesma forma. Porém, o trabalho de , nesse caso, é o trabalho de uma compressão isotérmica.
A gente calcula ele assim:
Como:
Então:
Pois é a temperatura é constante, de até
Chamando de a temperatura do ponto
A temperatura no ponto é:
E usando:
Assim:
Por fim, o trabalho total será:
Passo 4
Como vimos, o calor absorvido é o mesmo pros dois ciclos. Assim, a eficiência dos dois pode ser calculada por:
Assim:
Pra qualquer tipo de gás.
Assim:
d)
Resposta
d)