Escrever a Tag aqui (nome do capítulo IGUALZINHO), Outra tag, Mais uma tag
Dois alto-falantes A e B estão localizados no eixo como mostra a figura abaixo. Eles estão separados por uma distancia de . Cada alto-falante emite ondas sonoras em sentidos opostos, A no sentido e B no sentido , com frequências iguais a , e as fontes estão fora de fase em . A velocidade do som e . A que distancia do alto-falante A ocorrerá o primeiro ponto de interferência construtiva?
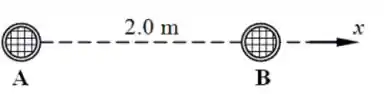
Passo 1
Para essa questão, basta a gente usar a fórmula:
Para uma interferência destrutiva, já que a diferença de fase entre as ondas é de
Para o primeiro ponto de interferência construtiva:
Além disso:
Assim:
Passo 2
Bom, descobrimos que a diferença entre as distâncias do ponto até as fontes é
Mas sabemos que:
Assim, somando as duas equações:
E assim:
Resposta
d)
Exercícios de Livros Relacionados
A figura mostra duas fontes pontuais F 1 e F 2 que emitem sons de comprimento de onda λ = 2,00m . As emissões são isotrópicas e em fase; a distância entre as fontes é d = 16,0m . Em qualquer ponto P s
Uma onda sonora senoidal se propaga no ar, no sentido positivo de um eixo x , com uma velocidade de 343 m / s . Em um certo instante, a molécula A do ar está em seu deslocamento máximo no sentido nega
Na figura abaixo temos as ondas sonoras A e B , de mesmo comprimento de onda λ , estão inicialmente em fase e se propagam para a direita, como indicam os dois raios. A onda A é refletida por quatro su
Duas ondas sonoras, produzidas por duas fontes diferentes de mesma frequência, 540H z , se propagam na mesma direção e no mesmo sentido a 330m / s . As fontes estão em fase. Qual é a diferença de fase
Na figura, um som com um comprimento de onda de 40,0c m se propaga para a direita através de um tubo que possui uma bifurcação. Ao chegar à bifurcação, a onda se divide em duas partes. Uma parte se pr