Escrever a Tag aqui (nome do capítulo IGUALZINHO), Outra tag, Mais uma tag
Duas cordas foram amarradas uma na outra com um no e depois esticadas entre 2 suportes rígidos, conforme a figura abaixo. As cordas têm densidades lineares e . Seus comprimentos são e . A tensao e a mesma em ambas as cordas e vale . Simultaneamente, um pulso e enviado a partir da extremidade rígida de cada corda em direção ao nó. O tempo para cada pulso chegar ao nó será:
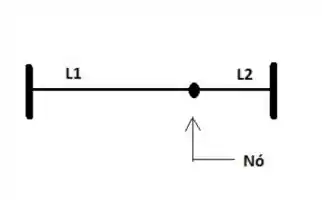
- Não é possível determinar os tempos sem conhecer a frequência das ondas nas cordas
Passo 1
Vamos primeiro calcular a velocidade de propagação das ondas de cada trecho:
Trecho 1:
Trecho 2:
Passo 2
Agora vamos calcular o tempo de cada um:
Trecho 1:
Trecho 2:
Assim:
Resposta
a)
Exercícios de Livros Relacionados
A figura mostra o deslocamento y do ponto de uma corda situado em x = 0 em função do tempot quando uma onda passa pelo ponto. A escala do eixo y é definida por y=6,0m m . A onda tem a forma y x ,t = y
Em um experimento com ondas estacionárias, uma corda de 90c m de comprimento está presa a um dos braços de um diapasão excitado eletricamente, que oscila perpendicuJarmente à corda com uma frequência
Uma onda senoidal transversal se propaga em corda no sentido positivo de um eixo x com uma velocidade de 80m / s . No instante t = 0 , uma partícula da corda situada em x = 0 possui um deslocamento tr
Na figura a , a corda 1 tem uma massa específica linear de 3,00g / m e a corda 2 tem uma massa específica linear de 5,00g / m . As cordas estão submetidas à tensão produzida por um bloco suspenso de m
A figura mostra a velocidade transversal u em função do tempo t para o ponto de uma corda situado em x = 0 , quando uma onda passa por ele. A escala do eixo vertical é definida por u s = 4,0m / s . A