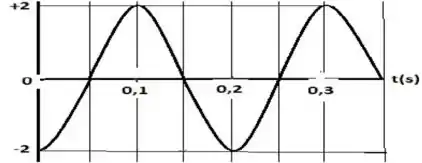
O gráfico-historia de uma onda senoidal que se desloca na direção positiva do eixo a , e mostrado na figura abaixo. A equação de deslocamento dessa onda é:
Passo 1
A equação básica de uma onda é:
Bom, pelo próprio gráfico, já podemos dizer que:
Passo 2
Agora é útil a gente calcular a frequência
Quanto vale Basta olhar no gráfico quando um ciclo inteiro da onda se repete, nesse caso:
Assim:
Com o valor de e o valor da velocidade dado no enunciado, podemos calcular
Assim, já temos:
O sinal na frente de se deve ao fato de que a onda se propaga na direção positiva de
Passo 3
Pra achar a constante de fase, basta a gente usar a equação da onda para que, como se pode ver no gráfico, precisa dar
Repare aqui que:
Assim:
Assim:
a)
Resposta
a)
Exercícios de Livros Relacionados
13.1. A corda de um piano emite um lá médio vibrando com uma frequência primaria igual a 220 Hz. a) Calcule o período e a frequência angular. b) Calcule a frequência angular de uma soprano emitindo um
Feixes de laser enviados para a Lua são um recurso rotineiro para se determinar com precisão a distância entre a Terra e a Lua. No entanto, para determinar a distancia com precisão, correções devem se
Use a equação de onda para determinar a velocidade de uma onda dada por y x , t = 3,00m m sen [ 4,00m - 1 x - 7,00s - 1 t ] .
Se, no exemplo 15.3 você não desprezasse a massa da corda, qual seria a velocidade da ondaNa extremidade inferior da corda;No meio da corda;Na extremidade superior da corda?
Um oscilador harmônico simples em x = 0 gera uma onda em uma corda. O oscilador opera em uma frequência de 40 H z e com uma amplitude de 3 c m . A corda possui uma densidade linear de 50 g / c m e est