Uma indústria química utiliza um hidrociclone para tratar de uma suspensão aquosa, a em volume de . Determine a eficiência de separação.
Dados:
, , ,
Configuração do hidrociclone:
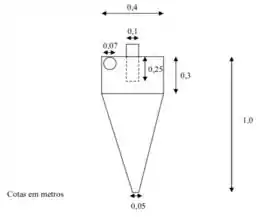
Passo 1
Temos que determinar a eficiência de separação obtida usando esse hidrociclone aí. Antes de qualquer coisa, temos que saber qual é a família desse hidrociclone pra saber quais equações e parâmetros usar. Lá na teoria, eu coloquei uma tabelinha com as proporções geométricas em cada uma das famílias. Vamos calcular para esse hidrociclone aí e ver se ele se encaixa em alguma família.
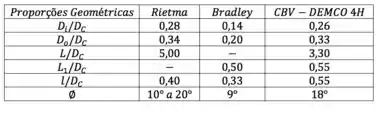
Calculando
Opa! Já sabemos que esse hidrocilone não tem família; ele é um hidrociclone qualquer então temos que usar as equações pra um hidrociclone qualquer.
E, para chegar na eficiência total de coleta: temos como, pelas equações, calcular ; como sabemos a expressão de em função de (vou usar a equação de Rosin-Rammler-Bennett modificada), teremos a expressão de “completa”. Depois, calculamos e depois .
Ah! Vou adotar o CGS então já vou listar os dados convertendo-os para o CGS, caso necessário:
Passo 2
Primeiro de tudo, vamos ter que calcular o diâmetro de corte reduzido, Em hidrociclones, trabalhamos majoritariamente com , e , e ficamos variando entre as definições e as correlações. Vou escrever aqui embaixo as duas formas (genéricas) de cada um deles (definição e correlação):
Repara que a expressão que envolve é a definição de ; daí podemos calcular pela correlação (termo da direita) e depois relacionar com a definição. Mas, antes disso, preciso de ; como não tenho , tenho que calcular pela correlação e, para isso, preciso de . Daí a primeira coisa que vou calcular é , certo? Tenho tudo da definição então é ela que vou usar:
Repara que eu lancei o em centímetros.
Calculando :
Calculando pela correlação:
Relacionando com a definição:
Substituindo os valores:
Passo 3
Vamos usar, para a expressão da eficiência granulométrica, a equação de Rosin-Rammler-Bennett modificada:
Com para hidrociclones
Já sabemos o valor de e de . A questão é que para encontrarmos o valor da eficiência global reduzida , vamos ter que integrar em :
Daí, precisamos de uma expressão para em função de . Vamos obtê-la da curva que o enunciado deu:
Aplicando dos dois lados:
Substituindo isso na equação de :
Agora, integramos na calculadora:
Mas o enunciado pede eficiência global e não a eficiência global reduzida ; sabemos que:
Daí:
Só uma análise do resultado: faz sentido ? Sim ! A vazão associada com a razão de fluido é como se tivesse de coleta, já que ela carrega partículas com a mesma distribuição original e isso faz com que a eficiência global do separador aumente.