Exercícios Resolvidos de Iminência de Virar um Corpo

Ver Teoria

Exercício 2 1 3

Enunciado

Um caixote cúbico uniforme tem de lado e pesa . Ele repousa em um piso com uma das arestas encostada em um obstáculo fixo muito pequno. A que altura mínima acima do piso deve ser aplicada uma força horizontal de para virar o caixote?

Passo 1

Primeiramente, vamos tentar entender melhor a figura:

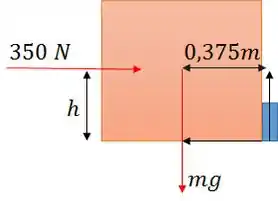
A altura mínima para virar o caixote é aquela que garante o equilíbro. Um infidesimal a mais, o caixote cúbico viraria.

Passo 2

Vamos aplicar então, as condições de equilíbrio! Sempre elas!

Escolhendo o eixo de rotação o aresta que encontra o obstáculo pequeno, podemos desconsiderar o torque gerado pela força do chão e pela força do obstáculo.

A distância perpendicular da força peso até a aresta do cubo é metade de . Vale .

A distância perpendicular da linha de ação da força aplicada até a aresta é

Convencionando o sentido anti-horário como positivo, podemos aplicar a equação do torque:

Resposta

Exercícios de Livros Relacionados

Para quebrar a casca de uma noz com um quebra nozes, forças de pelo menos 40 N de módulo devem agir sobre a casca em ambos os lados. Para o quebra-nozes da figura abaixo, com distânciaL = 12 c m e d =

Na figura de cima uma viga homogênea de 40,0k g repousa simetricamente em dois rolamentos. As distâncias entre as marcas verticais ao longo da viga são iguais. Duas das marcas coincidem com a posição

A figura da esquerda mostra uma rampa homogênea entre dois edifícios que leva em conta a possibilidade de que os edifícios oscilem ao serem submetidos a ventos fortes. Na extremidade esquerda, está pr

Na Fig. 12-71, uma viga homogênea com 60 N de peso e 3,2 m de comprimento está presa a uma dobradiça na extremidade inferior e uma força horizontal F → de módulo 50 N age sobre a extremidade superior.

Uma balança de pratos consiste em uma barra rígida de massa desprezível e dois pratos pendurados nas extremidades da barra. A barra está apoiada em um ponto que não fica no centro da barra, em torno d