Um lápis sextavado é colocado sobre um caderno (figura abaixo). Determine o menor coeficiente de atrito estático , tal que, se a capa do caderno for erguida, o lápis rolará para baixo sem escorregar.

Passo 1
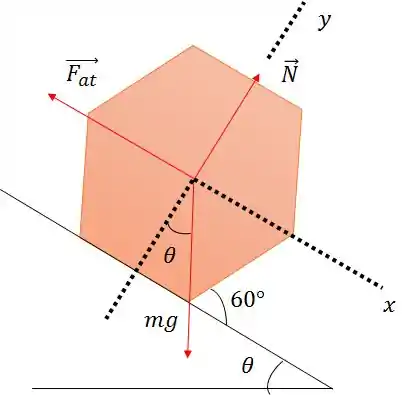
Vamos montar a figura do problema.
Temos a força de atrito, a força normal e a força peso. Fica mais fácil colocar o eixo xy na direção da força de atrito e normal, porque assim já contemplamos duas forças.
Dá para fazer uma manipulação rápida ali e transferir o para a componente do peso.
O ângulo interno de um hexágono é regular é e o ângulo externo é .
Passo 2
Na situação limite do rolamento, ainda temos as condições de equilíbrio. Isso significa que o torque resultante em relação a qualquer ponto ainda deve ser zero. Nessa situação, o lápis fica apoiado somente no ponto A, indicado na figura abaixo.
Assim, se quisermos que o lápis esteja na iminência de rolar sem escorregar, é necessário que o centro de massa esteja acima do ponto A, ou seja esse ponto e o centro de massa ligados geram uma reta vertical. Dessa forma, ao aplicarmos o torque em relação a esse ponto, ele ainda será igual a zero (já que as forças normal e atrito estarão nesse ponto e a força peso tem como direção uma reta que passa por esse ponto).
Dando um zoom para explicar isso. Olha como fica!
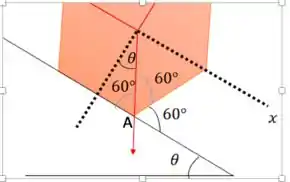
Assim, vemos que o ângulo crítico, ou seja, na iminência dele girar é de .
Se aumentássemos um pouquinho só esse ângulo, o lápis já viraria.
Passo 3
Agora, precisamos relacionar o ângulo com o coeficiente de atrito .
Vamos aplicar as condições de equilíbrio, já que como estamos falando do menor coeficiente de atrito, estamos falando, também, de iminência.
Então, aplicamos
Passo 4
Para isso, vamos decompor nos eixos e .
Passo 5
Depois de já decompomos, fica mais fácil. Se liga:
Como queremos relacionar com , precisamos colocar o coeficiente de atrito na história.
Você se lembra que ? Então, vamos usar isso aqui.
Sabemos que o ângulo crítico da iminência é .
Logo o mínimo é