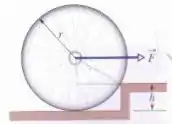
Na figura abaixo, qual é o menor valor do módulo da força horizontal (constante) , aplicada horizontalmente ao eixo da roda, que permite à roda ultrapassar um degrau de altura ? O raio da roda é e a massa .
Passo 1
Primeiramente, vamos entender as forças que atuam no problema.
A gente desconsidera força normal na base da roda, porque a força mínima vai ser o ponto que essa normal é zero.
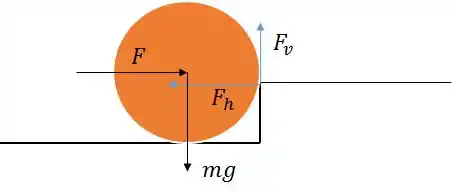
Passo 2
Sabemos que como o mínimo de força é aplicado, a roda não vai apresentar aceleração.
A força mínima é um infidesimal maior do que a força que a força que garante o equilíbrio. É como se a gente colocasse uma formiga na situação de equilíbrio e a roda andasse.
Como não tem aceleração, a força resultante é zero. E... Podemos usar as equações de equilíbrio!
Vamos calcular o torque resultante no ponto em que a roda toca na quina.
Repare só na figura.
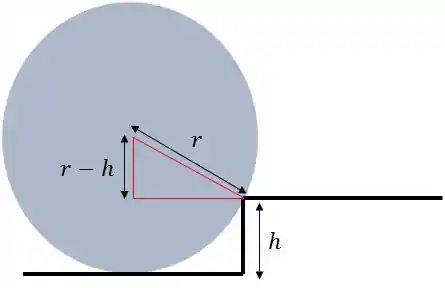
Show!
Quando calculamos o torque resultante nesse ponto, já sabemos que o torque gerado por e são nulos.
Temos que achar o torque gerado por e por .
A distância perpendicular da linha de ação de até o eixo é de .
A distância perpendicular da linha de ação de mg até o eixo é o outro cateto. Sabemos que por Pitágoras, ele vale:
Passo 3
Opa! Falta só aplicar a equação do torque. Considerando o sentido anti-horário positivo.
Podemos substituir os valores do problema.