Segundo a Lei de Faraday-Neumann, uma força eletromotriz é induzida em um circuito ou objeto semelhante a circuito elétrico sempre que há variações do fluxo magnético, sendo a força dada pela taxa de variação do fluxo magnético em função do tempo.

Levando em conta a Lei de Faraday, considere um avião de de comprimento entre as extremidades de suas asas, voando a através de um campo magnético terrestre uniforme e de intensidade igual a . Nesse contexto, calcule a induzida entre as extremidades das asas.

Relembrando que o fluxo magnético nada mais é do que o produto entre:

O campo magnético foi dado no enunciado:

Então:

Mas quem é a nossa área? Bom entre as asas nós temos a medida de que se movem a uma velocidade de . Pense numa espira retangular:

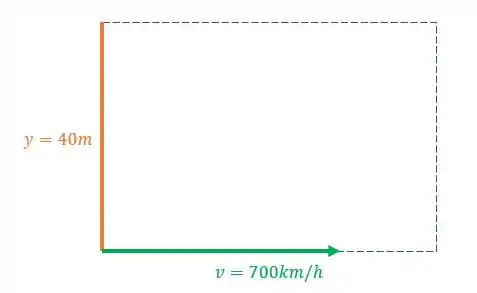
Onde mantemos a medida da espira igual a , enquanto variamos a sua largura com a velocidade. Logo a área seria:

Provoca o fluxo elétrico:

Substituindo no cálculo da :

Sabemos que a medida da espira tem valor fixo:

Podemos então retirar todos os valores fixos de dentro da derivada:

Quem será essa derivada da posição em relação ao tempo? É a velocidade que a posição varia, que sabemos que é igual a:

Como sabemos que não podemos utilizar a velocidade em e sim em devemos fazer essa transformação. Basta dividir o valor por :

Vamos colocar isso na equação da :

Realizando essa conta, temos o produto entre os números do numerador:

Dividindo por , teremos:

Para terminar essa questão basta sumir com essa potência de , para isso temos que mover a vírgula para a esquerda casas:

Que é aproximadamente igual a:

Nossa resposta final!