Calcule a velocidade superficial de água e que passa através do meio poroso abaixo, sabendo-se que este leito foi constituído por de areia com diâmetro de . Admitir que o escoamento é darcyano.
Dados:
- Diâmetro do leito:
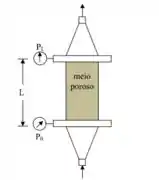
Passo 1
Essa é uma instalação bem simples: só tem o meio poroso.
Então, vamos começar caracterizando esse meio poroso, calculando e :
Para a porosidade:
Repara que usamos o SI e é fundamental que as unidades sejam iguais, para que a porosidade seja admensional!
Agora, bora calcular a permeabilidade do meio poroso :
Considerando que a areia possa ser aproximada por grãos, podemos usar . Daí:
Repara que a gente usou o diâmetro da partícula em metros, pra trabalhar no SI. A unidade que você usar no diâmetro vai definir a unidade do , já que as outras variáveis usadas são adimensionais.
Depois de achar os parâmetros do nosso meio poroso, podemos olhar pra geometria do problema e aplicar a equação de Bernoulli, já que o fluido é incompressível.
Passo 2
Aplicando a equação de Bernoulli:
Agora bora simplificar a equação, adotando o ponto como a entrada e como a saída:
- Podemos escrever a vazão como ; como vazão e área são constantes, é constante daí
- Não há bomba, daí
- , conforme vimos na teoria
Então a nossa equação simplificada ficou:
Adotando o SI:
Daí:
Como o escoamento é lento, vale a lei de Darcy:
Ainda no SI: