Estimar a capacidade, em , do filtro de areia abaixo esquematizado operando com água a . A primeira camada, com porosidade , é constituída de areia com a seguinte granulometria:
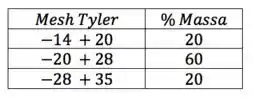
A segunda camada, como porosidade , é constituída de brita com partículas de de diâmetro. As esfericidades da areia e da brita podem ser consideradas como .
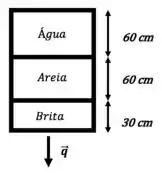
Observação: o filtro é aberto pra atmosfera tanto na entrada como na saída!
Passo 1
Vou usar subscrito para areia, para brita e chamar a água de água mesmo haha.
O enunciado dá um filtro com três camadas e pede pra calcularmos a capacidade, em , isto é, temos que calcular .
Algo importante é que sabemos (o enunciado diz) que o filtro é aberto pra atmosfera tanto na entrada como na saída, ou seja:
Passo 2
Considerando o eixo no mesmo sentido da velocidade , a equação do movimento fica:
Passando para o outro lado,
Primeiro de tudo, vamos considerar que não há perda de carga ao passar pela camada de água; isso é razoável e, de qualquer maneira, nem teríamos como estimar essa perda. Depois, vamos avaliar essa equação em cada um dos trechos.
- Para a areia:
- Para a brita:
- Para areia:
- Para a brita:
Em que:
Resolvendo a integral, temos:
Como,
Substituindo isso em , temos:
O que nos dá ! Para simplificar, vou chamar de .
Substituindo na equação 1, temos:
Sendo,
E de forma semelhante, chegamos em:
Chamei de para simplificar!
Somando as equações , eliminamos o “intermediário”, que é :
Acontece que p filtro é aberto pra atmosfera na saída, daí:
E, como desconsideramos perda de carga na camada de água, é como se fosse fluido estático, daí:
Daí:
Guarda isso por enquanto, ok?
Passo 3
Precisamos das expressões do . Como enunciado NÃO fala que escoamento é lento, usamos Forchheimer:
Epa! Não temos ; temos que determiná-los. Como não temos experimentos, usamos as correlações.
Para :
Repara que é o diâmetro médio de Sauter e foi calculado com os dados daquela tabelinha que o enunciado deu.
Para calcular , usamos a correlação de Santana e Massarani:
Em que e essa correlação é válida para valores de entre:
Daí:
Substituindo os nas expressões de e substituindo essas na equação que pedi pra você guardar:
Resolvendo a equação de segundo grau gerada:
A segunda opção NÃO tem sentido físico. Sabemos que o fluido tem que descer, por causa da gravidade, e dissemos que o sentido positivo do eixo z é para baixo, daí tem que ser positivo. Daí:
Como o enunciado pede nas unidades , convertemos e: