Simplifique a equação do movimento para achar uma expressão para a queda de pressão no meio poroso em cada um dos casos abaixo:
- Escoamento contra a gravidade
- Escoamento perpendicular à gravidade
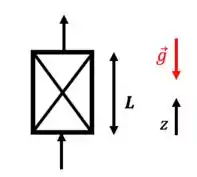
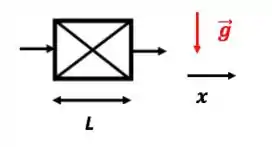
Despreze o termo da equação do movimento!
Passo 1
Nessa questão vamos ter que manipular a equação do movimento pra achar uma expressão pro em cada um dos meios porosos apresentados. Temos o caso de uma instalação que apenas tem o meio poroso, daí a única perda que carga com a qual teremos que nos preocupar é o .
Vamos ter que usar a equação do movimento então bora logo lembrar dela:
Ah, o enunciado pede pra desprezar o termo da equação do movimento, então vou tirá-lo logo.
Ignorá-lo é uma boa aproximação... ele fica pequeno face aos outros termos.
Agora, indo pra parte que diferencia os dois casos: no primeiro caso vamos estar interessados na componente do movimento, pois é nela que o movimento se concentra, exclusivamente. Como a gravidade também se encontra nesse eixo, ela vai aparecer no equacionamento.
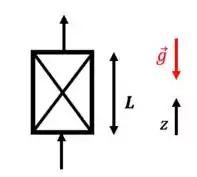
Já no segundo caso, o movimento é no eixo ; como a gravidade NÃO está presente nesse eixo, ela NÃO aparecerá no equacionamento, ou melhor, terá valor zero. Daí o termo será nulo.
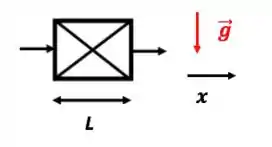
Passo 2
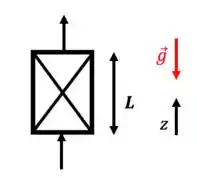
- Escoamento contra a gravidade
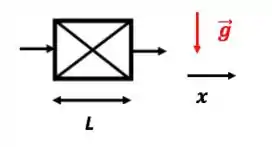
- Escoamento perpendicular à gravidade
Voltando à equação do movimento, já desprezando :
Antes de continuar, mais uma simplificação: NÃO nos foram informadas variações no tempo e nem variações do espaço, daí, vamos usar as hipóteses de estado estacionário e meio isotrópico. Razoável, né?
Só há movimento no eixo z, daí vamos escrever apenas a componente dos vetores para esse eixo.
Podemos isolar o termo com nessa equação:
Jogando o pra direita e integrando de até (repara que eu disse que o zero do meu eixo é onde começa o meio poroso):
Passo 3
Novamente, vou usar as hipóteses de estado estacionário e meio isotrópico.
O lance é que, agora, o movimento ocorre exclusivamente ao longo do eixo x. Daí vamos escrever as componentes dos vetores apenas para esse eixo. E, como já adiantei no passo 1, a componente da gravidade nesse eixo é ZERO. Daí:
Isolando o :
Integrando, em x, de a :