Encontre a expressão para perda de carga no meio poroso:
- Escoamento contra a gravidade
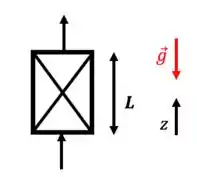
Despreze o termo da equação do movimento!
Passo 1
Como vimos na teoria, para encontrar uma expressão para perda de carga no meio poroso , precisamos usar tanto a equação do movimento como a equação de Bernoulli; encontramos um ponto de amarração, isto é, um termo igual nas duas equações e usamos ele para igualar expressões e depois isolar .
Já vimos em exercício anterior como fica o desenvolvimento da equação do movimento para esse caso:
- Escoamento contra a gravidade
Então, vou concentrar, nesse exercício, em trabalhar Bernoulli e o isolamento de .
Passo 2
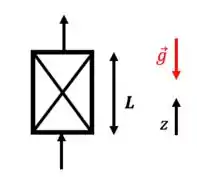
A equação do movimento simplificada para este caso é:
Indo pra Bernoulli, a equação geral é:
Repara que estou usando subscrito para o início do meio poroso e para o fim.
Podemos simplificar Bernoulli:
- O diâmetro por onde o fluido passa é constante daí área transversal é constante; como , é constante
- Não tem bomba então não tem como ter trabalho da bomba né. Daí
A diferença de alturas vale e o se resume ao , que chamei de :
Passo 2
Agora temos que juntar as duas equações:
Equação do movimento:
Bernoulli:
Substituindo a primeira na segunda: