Com base no conjunto de pontos abaixo, resolva a interpolação inversa usando a primeira abordagem de resolução do capítulo. Escolha o método que achar necessário para a resolução do polinômio. Além disso, encontre se :

Passo 1
Antes de iniciar a resolução do problema, vale atentar que estamos usando calculadoras diferentes e arredondamentos diferentes, o que pode acarretar pequenas divergências no resultado final, mas se chegar próximo ao que calculamos aqui já está bem aceitável!!!
Vamos encontrar um polinômio que interpole em e depois achar tal que , sendo necessário achar a raiz do polinômio (por qualquer outro método já estudado para encontrar raízes ).
Como temos 3 pontos, podemos montar um polinômio de grau 2:
Podemos resolver por eliminação de Gauss, onde:
Utilizando as regrinhas de Eliminação de Gauss iremos substituir a linha 2, visando zerar o termo :
O mesmo processo deve ser feito para a linha 3:
A nova matriz atualizada é:
Agora, devemos zerar o termo !
Passo 2
Faremos o mesmo processo que o usado anteriormente:
Utilizando as regrinhas de Eliminação de Gauss iremos substituir a linha 2, visando zerar o termo :
Usanto retrosubstituição, ficamos com:
O polinômio pode ser construído :
Passo 3
O exercício pede: se
Podemos resolver essa equação de segundo grau por Bhaskara:
Se:
Com essa equação, conseguimos dois valores para :
Temos dois valores para , agora vamos analisar novamente a tabela:
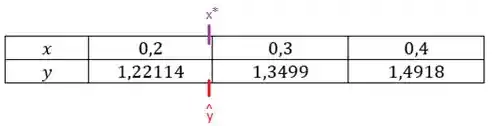
Observe que sabemos o valor de que está dentro do intervalo [1,22114; 1,3499]. Isso significa que o valor requerido de deve estar entre [0,2 ; 0,3]. Com isso, podemos excluir o valor por estar fora do intervalo [0,2 ; 0,3].
Sendo assim para o valor de .
Resposta
o valor de .