Com base no conjunto de pontos abaixo, resolva a interpolação inversa usando a segunda abordagem de resolução do capítulo utilizando a inversão de termos, encontre o valor de quando :
Passo 1
O primeiro passo é trocar os valores de por :
Passo 2
Com base nesse conjunto de pontos, podemos montar a tabela de diferenças divididas e montar o polinômio interpolador, utilizando o método de Newton:
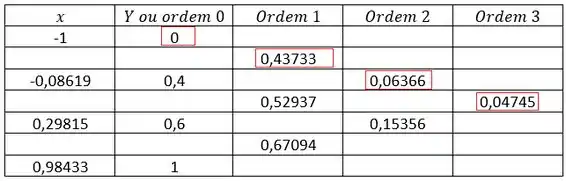
Agora, ficamos com :
Passo 3
O polinômio interpolador passa a ser:
Se:
Se
Resposta
0 o valor de
Exercícios de Livros Relacionados
17. Considere a tabela abaixoUsando um polinômio interpolador de grau 3, determine x tal qual f x = 2 . 3 . Justifique a escolha do processo.