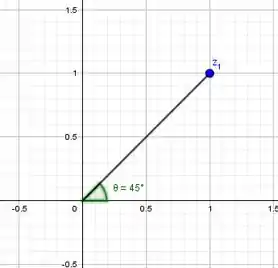
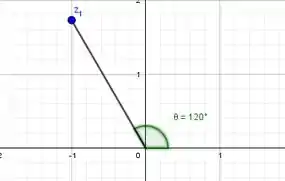
Dados os complexos a seguir, determine o módulo e o argumento dos respectivos, além de representa-los no plano complexo de Argand-Gauss.
Passo 1
Faaaaala aí, melhor aluno de Pré-Cálculo! Para resolver essa questão, vamos precisar lembrar da fórmula de módulo e argumento, mas não se preocupe, porque eu estou aqui para isso hahaha
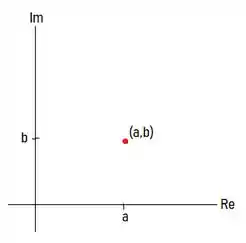
Dado um complexo da forma:
Onde são reais, temos que:
E além disso:
E sua representação no plano Argand-Gauss:
Passo 2
Bora começar do começo!
Vamos começar representando esse complexo no gráfico, para que fique melhor a visualização:
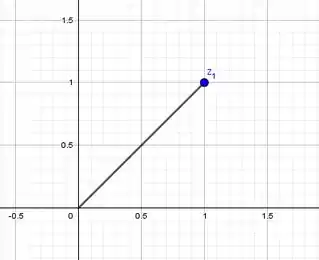
Bom, para calcular o módulo, temos que:
Então:
Agora que achamos o módulo, vamos em busca da última coisa: o argumento!
Segue que:
Então os ângulos de a que possuem tangente igual a são:
Porém, repare que nosso argumento está no primeiro quadrante, já que ele é o ângulo entre o eixo real e o segmento da origem ao complexo.
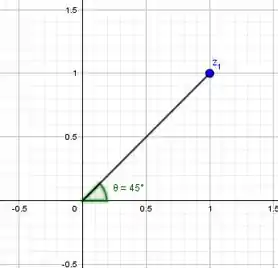
Então .
Passo 3
Vamos começar representando esse complexo no gráfico, para que fique melhor a visualização:
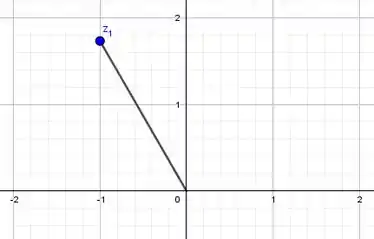
Bom, para calcular o módulo, temos que:
Então:
Agora que achamos o módulo, vamos em busca da última coisa: o argumento!
Segue que:
Então os ângulos de a que possuem tangente igual a são:
Porém, repare que nosso argumento está no segundo quadrante, já que ele é o ângulo entre o eixo real e o segmento da origem ao complexo.
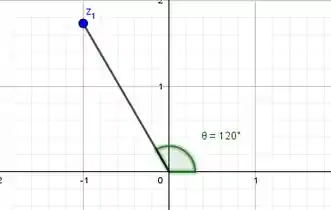
Então .
Passo 4
Resposta