Represente os seguintes números complexos na forma polar:
Passo 1
Bom, colocar complexos na forma polar é fazer:
Onde:
Então ele é equivalente a forma trigonométrica, só que aqui utilizamos a identidade de Euler:
Bora colocar a mão na massa!
Passo 2
Primeiramente, precisamos do seu módulo:
Agora vamos em busca do seu argumento:
Precisamos pensar nos ângulos de a que possuem tangente igual a . Eles são:
Porém, perceba que representando nosso complexo graficamente:
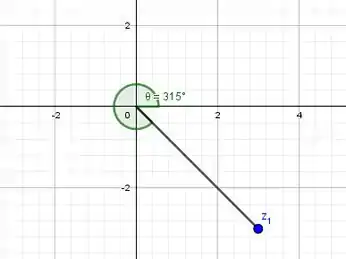
Então e a representação polar do complexo será:
Passo 3
Primeiramente, precisamos do seu módulo:
Agora vamos em busca do seu argumento:
Precisamos pensar nos ângulos de a que possuem tangente igual a . Eles são:
Porém, perceba que representando nosso complexo graficamente:
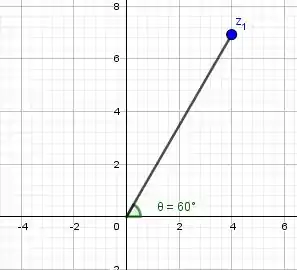
Então e a representação polar do complexo será: