Escreva os seguintes números complexos na forma trigonométrica:
Passo 1
Bom, primeiro de tudo é saber escrever um complexo na forma trigonométrica. Dado um complexo:
Sua forma trigonométrica é:
Onde e . Bora começar!
Passo 2
Calculando seu módulo:
E agora vamos acha seu argumento:
Como isso não existe, precisamos calcular o limite:
Então, precisamos pensar quais ângulos de a que possuem tangente tendendo pro infinito. Esses são:
Porém, olhe a representação do nosso complexo no plano:
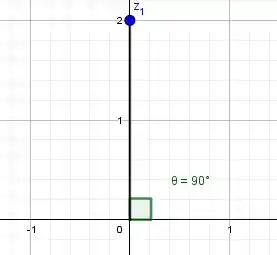
Então .
Agora que já temos nossos módulo e argumento, bora representação trigonometricamente o complexo:
Passo 3
Calculando seu módulo:
E agora vamos acha seu argumento:
Então, precisamos pensar quais ângulos de a que possuem tangente igual a . Esses são:
Porém, olhe a representação do nosso complexo no plano:
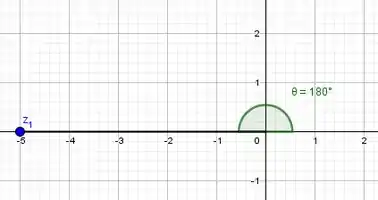
Portanto, .
Agora que já temos nossos módulo e argumento, bora representação trigonometricamente o complexo:
Passo 4
Calculando seu módulo:
E agora vamos acha seu argumento:
Então, precisamos pensar quais ângulos de a que possuem tangente igual a . Esses são:
Porém, olhe a representação do nosso complexo no plano:
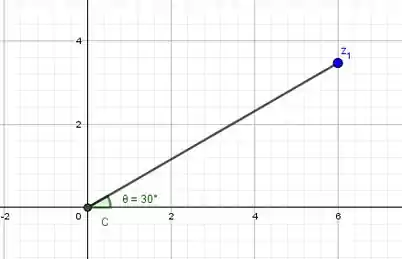
Portanto, .
Agora que já temos nossos módulo e argumento, bora representação trigonometricamente o complexo: