Uma tira de aço L2 com 3 mm de espessura e 50 mm de largura é curvada até formar um arco circular de 15m de raio. Determine a tensão de flexão máxima da tira.
Passo 1
Fala aí, pessoal! Antes de mais nada vamos fazer um desenho desse problema para ficar mais fácil de entender:
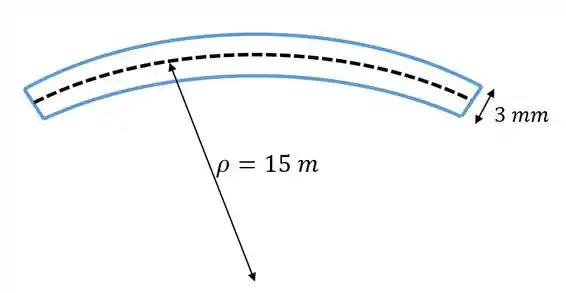
Perceba que ocorre uma flexão e por causa disso existe uma tensão de flexão associada e é isso que o problema nos pede!
Passo 2
A tensão de flexão é dada pela letra e pode ser calculada de diversas formas. A principal delas é:
Onde:
- é o momento fletor.
- a maior distância entre a linha neutra e o ponto que estamos calculando.
- o momento de inércia da seção transversal.
- é o momento fletor.
- é o módulo de elasticidade do material.
- o momento de inércia da seção transversal.
Mas a gente não tem o momento fletor! Temos apenas o raio de curvatura :
Esse dado vai nos ajudar me muito porque podemos achar o momento fletor através do raio de curvatura com a equação:
Onde:
Associando as duas equações vamos ter:
Perceba que temos todas essas grandezas! Agora basta substituir!!
Passo 3
Vamos fazer essa substituição! Observando que, para o aço L2 temos e a distância é a maior distância entre a linha neutra (linha preta pontilhada na figura) e a superfície, dessa forma:
obs: Pegamos o maior valor de porque queremos a máxima tensão de flexão, beleza? Quanto maior o maior o !
Substituindo: