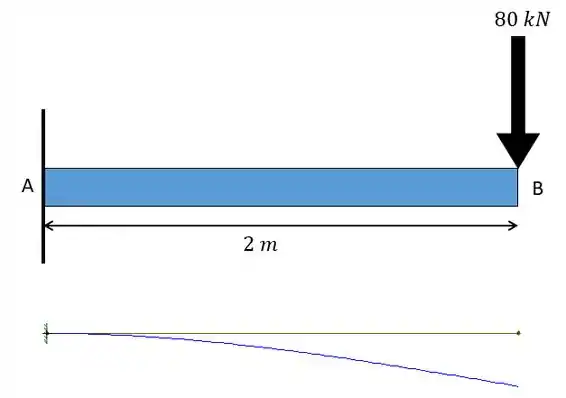
Para a viga de aço (E=200 GPa) e carregamento mostrado a seguir determine o raio de curvatura na metade da viga, faça também um esboço da linha elástica. Dados: Momento de inércia da barra
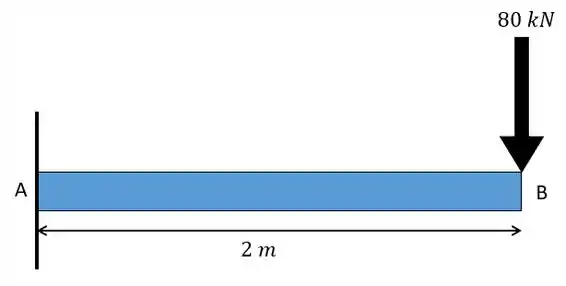
Passo 1
Fala ai, pessoal!! Esse problema começa a introduzir o conceito de linha elástica e pede o esboço dela e o raio de curvatura na metade da viga. Para fazer isso a gente só precisa saber de como os apoios reagem (são as condições de contorno) e achar o momento fletor na barra.
Precisamos basicamente de duas coisas então: as condições dos apoios e o momento.
Passo 2
Vamos olhar as condições de contorno. Para as condições de contorno sempre vamos analisar duas coisas: o ângulo e a posição. Neste caso temos um engaste em e uma extremidade livre em logo as condições são dadas como:
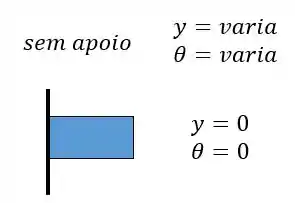
Com isso podemos desenhar a linha elástica:
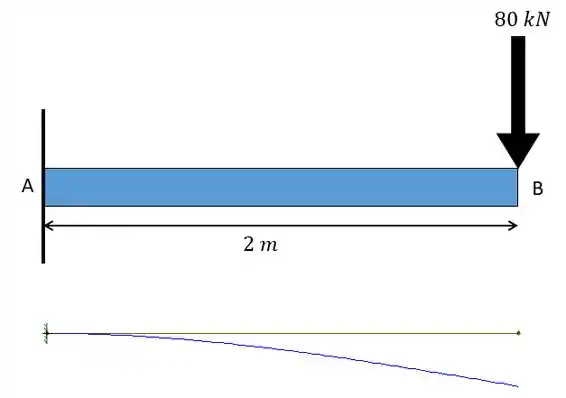
Perceba que a barriga está sempre voltada para baixo, o engaste não possui variação nem de altura nem de angulação enquanto o ponto livre possui variação de ambos.
Então já temos o nosso esboço da linha elástica! Vamos descobrir o raio de curvatura!
Passo 3
Para achar o raio de curvatura temos de achar o momento fletor, para isso vamos fazer um esquema das forças atuantes e para que o sistema se mantenha em equilíbrio vamos ter a seguinte configuração:
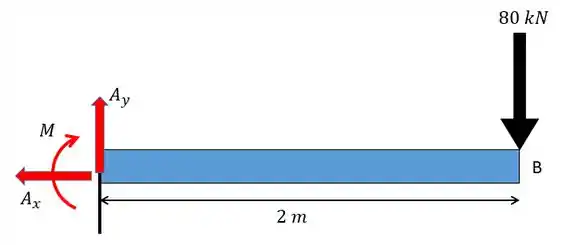
Utilizando as equações de equilíbrio estático vamos obter:
Para :
Para o momento em relação ao ponto e considerando o sentido horário positivo:
Assim podemos achar o momento fletor numa seção qualquer.
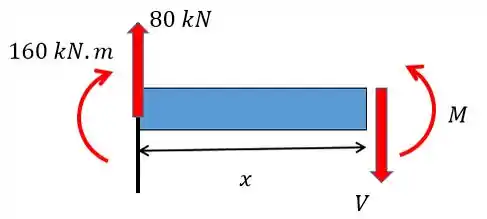
Para achar o momento fletor basta fazer o somatório de momentos em realção ao ponto :
Como a força cortante é igual à força de mas negativa vamos ter:
Assim o diagrama de momento fletor fica da forma:

Bom, na verdade a gente nem precisa fazer o diagrama, mas é legal para perceber que o momento fletor sempre vai ser positivo, isso indica que a linha elástiva sempre vai ter a barriguinha apontada para baixo (ou seja, nosso esboço estava certo! Uhulll)))
Passo 4
Agora vamos achar o raio de curvatura no ponto média da barra. O raio de curvatura pode ser calculado como:
Como queremos o momento fletor em :
E agora é só utilizar os dados da questão:
Resposta