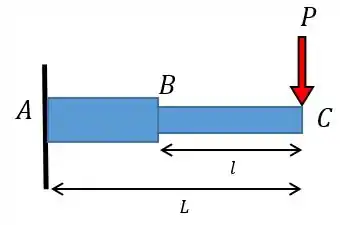
A viga é composta por duas hastes e está sujeita à carga concentrada . Os momentos de inércia são e e o módulo de elasticidade é . Explique o que a diferença entre os momentos de inércia implicam no cálculo do raio de curvatura da nossa viga. Um momento de inércia maior aumenta ou diminui o raio de curvatura? E se fosse o caso de coeficientes de elasticidade diferentes, haveria mudança em ?
Passo 1
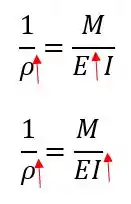
Vamos lá galerinha! Essa questão exige um pouquinho de conhecimento da fórmula do raio de curvatura, que é dada por:
Então o raio de curvatura vai depender do momento fletor , do momento de inércia e do coeficiente de elasticidade . O que a questão pede é saber o que acontece com quando variamos e ?
Passo 2
A primeira coisa que devemos entender é que o momento fletor depende apenas do carregamento, ou seja, nem o momento de inércia e nem o coeficiente de elasticidade interferem no valor de .
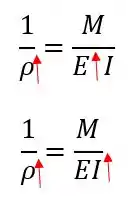
Aí olhando para a equação a gente pode ver que tanto quanto são diretamente proporcionais à , portanto quando há um aumento tanto do momento de inércia quanto do coeficiente de elasticidade ocorre um aumento do raio de curvatura:
Galera, é importante perceber que quanto maior for o raio de curvatura então menor será a curvatura da nossa viga, olha só:
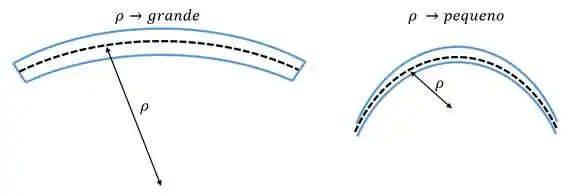
Isso faz sentido correto? Já que um material muito duro ( elavado) vai se deformar menos do que um material macio.
A mesma coisa vale para o momento de inércia. Um blocão de alumínio tem uma curvatura menor do que uma fitinha de alumínio, quando submetidos ao mesmo carregamento.
Resposta
Quanto maior o coeficiente de elastividade e/ou o momento de inércia então maior será o raio de curvatura.