Esboce o lugar geométrico das raízes e suas assíntotas para o sistema mostrado abaixo:
Passo 1
Essa função de transferência apresenta um zero, , e um polo, . Vamos começar representando eles em nosso diagrama:
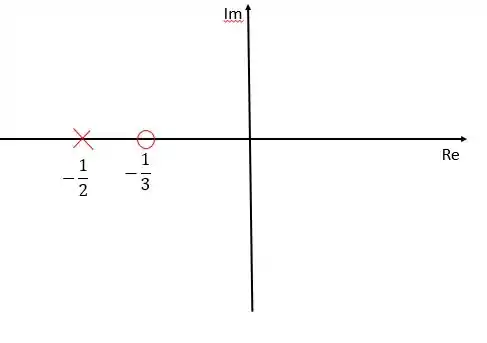
Passo 2
Essa função de transferência tem o mesmo número de polo e de zeros, ou seja, não existe nenhum zero no infinito, e portanto, não precisamos calulcar as assíntotas para determinar esse zero.
Sendo assim, já podemos representar nossos ramos. Lembrando sempre de observar todas as regrinhas.
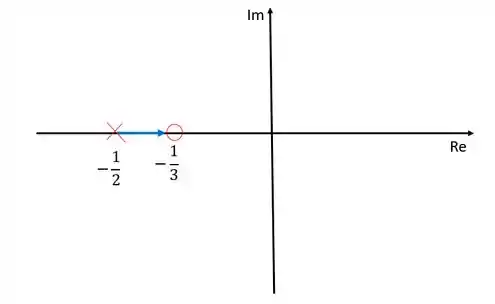
O número de ramos é igual ao número de polos, nesse caso então, só teremos um ramo.
Só pode existir um ramo se à esquerda dele existir um número ímpar de polos e zeros. Ou seja, à direita de não existe ramo pois nesse intervalo não existe nenhum zero ou polo à esquerda e à esquerda de também não pode ter ramo porque nesse intervalo existe um zero e um polo à esquerda, dando um total de dois que é um núemero par.
Outra regra importante é que todo ramos nasce em um polo e morre em um zero. Como só temos um polo e um zero, nosso diagrama ficará da seguinte forma:
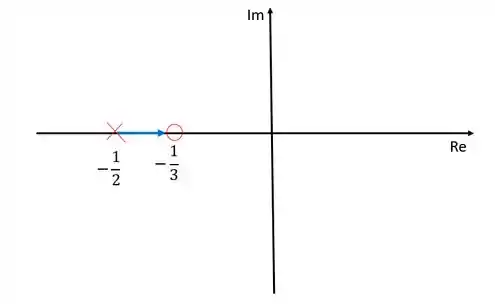
Repare que dessa forma, todas as regras foram obedecidas.
Resposta