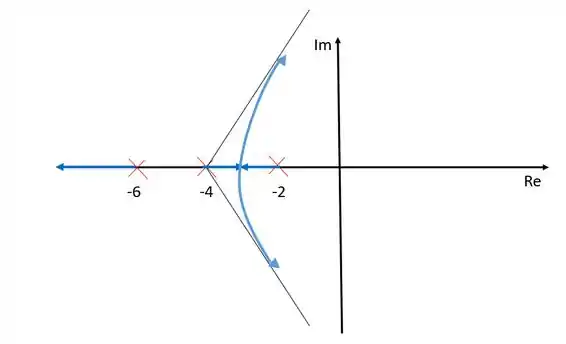
Esboce o lugar geométrico das raízes e suas assíntotas para o sistema mostrado abaixo:
Passo 1
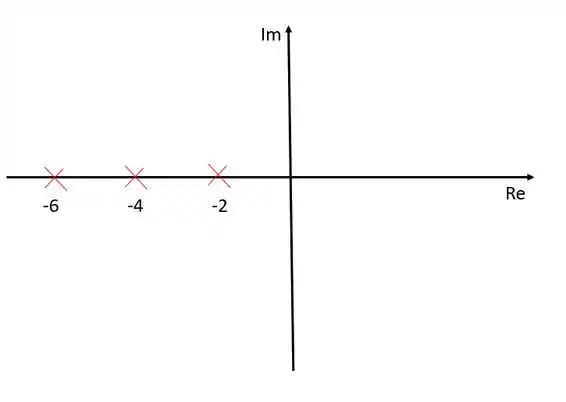
O primeiro passo para montar o nosso esboço do lugar das raízes sempre será identidicar os polos e zeros da nossa função de transferência e representa-los no diagrama.
A função de transferência do exercício não apresenta zeros porém possui três polos, , e .
Passo 2
Agora, vamos aplicar as nossas fórmulas para encontrar o ângulo das assíntotas com o eixo dos reais e em que ponta elas vão interceptar esse eixo:
Podemos perceber que se for igual a o ângulo será , se for , será , e se for será . Repare que se continuarmos aumentando o valor de esses valores vão se repetir.
Agora vamos calcular onde a assíntota intercepta o eixo real:
Coocando no diagrama de lugar das raízes:
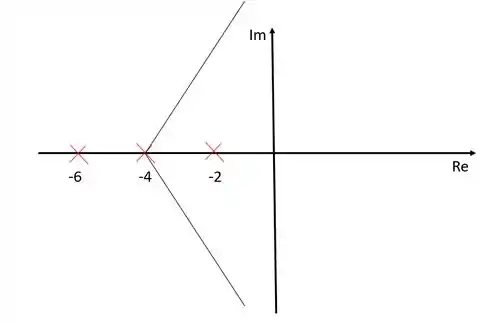
Estão representadas as assíntotas com inclinação e . A assíntota com inclinação está localizada sobre o eixo dos reais.
Passo 3
Agora devemos começar a representar os ramos. Os ramos sempre começam nos polos e terminam nos zeros. Como nesse caso não temos zeros finitos, nós precisaremos que os polos terminem nos zeros no infinitos, ou seja, precisaremos de três zeros no infinito.
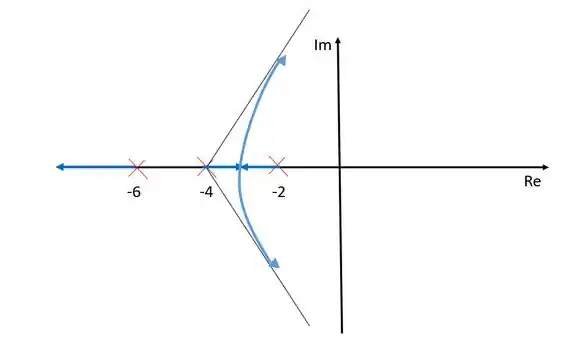
Entre e e entre e não podem existir ramos sobre o eixo real pois nesses lugares estão à esquerda de um número par de zeros e polos. Dessa forma ficamos com um ramo saindo do polo e vai para o infinito negativo real, e outros dois ramos saindo de e que se encontram deixam o eixo dos reais tendendo aos zeros no infinito indicados pelas assíntotas.
Resposta