Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lugar geométrico das raízes

Ver Teoria
Exercício 81234567

Enunciado

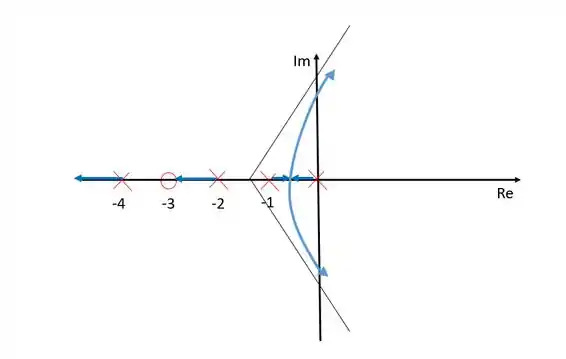
Esboce o lugar geométrico das raízes para o sistema mostrado abaixo:

G s = K s + 3 s s + 1 s + 2 s + 4

Passo 1

O primeiro passo para montar o nosso esboço do lugar das raízes sempre será identidicar os polos e zeros da nossa função de transferência e representa-los no diagrama.

A função de transferência do exercício apresente um zero, - 3 , e quatro polos, 0 , - 1 , - 2 e - 4 :

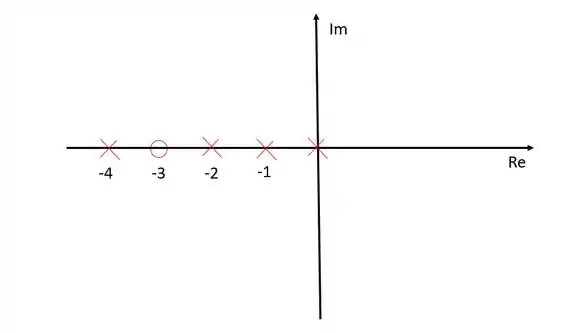
Passo 2

Agora, vamos aplicar as nossas fórmulas para encontrar o ângulo das assíntotas com o eixo dos reais e em que ponta elas vão interceptar esse eixo:

θ a = ± 180 2 r + 1 n º   d e   p o l o s   f i n i t o s - n º   d e   z e r o s   f i n i t o s =   ± 180 2 r + 1 4 - 1 = 60 ( 2 r + 1 )

Podemos perceber que se   r for igual a 0 o ângulo será 60 º , se for 1 , será 1 80 º , e se for 2 será 300 º . Repare que se continuarmos aumentando o valor de r esses valores vão se repetir.

Agora vamos calcular onde a assíntota intercepta o eixo real:

σ a = ∑ p o l o   f i n i t o s - ∑ z e r o s   f i n i t o s n º   d e   p o l o s   f i n i t o s - n º   d e   z e r o s   f i n i t o s = - 4 - 2 - 1 - 0 - - 3 4 - 1 =   - 4 3

Coocando no diagrama de lugar das raízes:

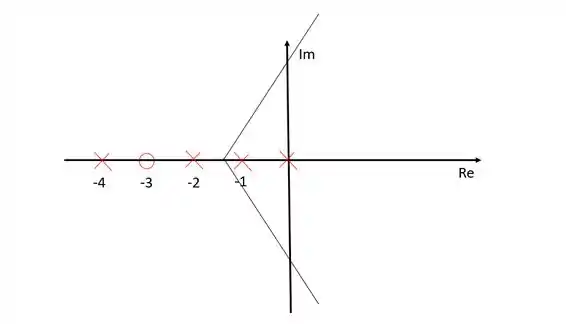
Estão representadas as assíntotas com inclinação 60 º e 300 º . A assíntota com inclinação 180 º está localizada sobre o eixo dos reais.

É importante ressaltar que as assíntotas não fazem parte do diagrama de lugar das raízes, elas apenas indicam onde estão localizados os zeros no infinito do sistema. Como nesse caso temos três polos a mais que zeros, precisaremos de três zeros no infinito.

Passo 3

Agora devemos representar de fato as linhas do lugar das raízes (os ramos). Primeiramente devemos lembrar que a quantidade de ramos é igual à quantitade do número de polos do sistema. Os ramos sempre começam em um polo e terminam em um zero e sempre estão localizados à esquerda de um número ímpar de par ou polos no eixo real. Sendo assim:

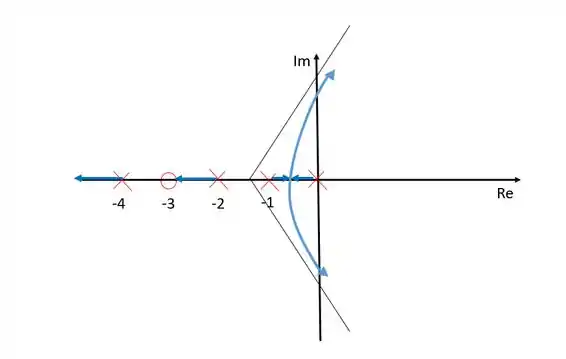
Repare que entre - - 1 e - 2 e entre - 3 e - 4 não existe nenhum ramo pois eles estão a esquerda de um número par de polos e zeros. Todos os ramos começam em polos e terminam em zeros e que existem três zeros no infinito.

Resposta