Esboce o lugar geométrico das raízes e suas assíntotas para o sistema mostrado abaixo:
Passo 1
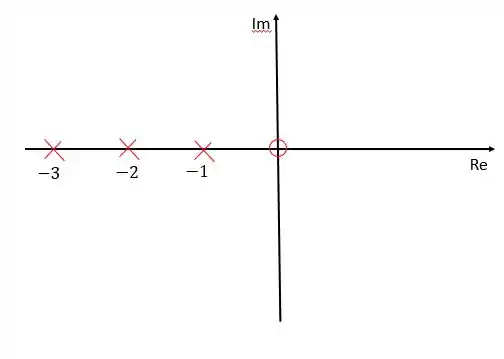
Essa função de transferência apresenta um zero em e três polos em , e .
Representando esses polos e zeros no diagrama de lugar das raízes:
Passo 2
Nesse caso temos dois polos a mais que zeros, então teremos dois zeros no infinito. Precisamos então calcular nossas assíntotas:
A assíntota terá inclinação se for igual , e se for igual a 1. Após isso, os valores começam a se repetir.
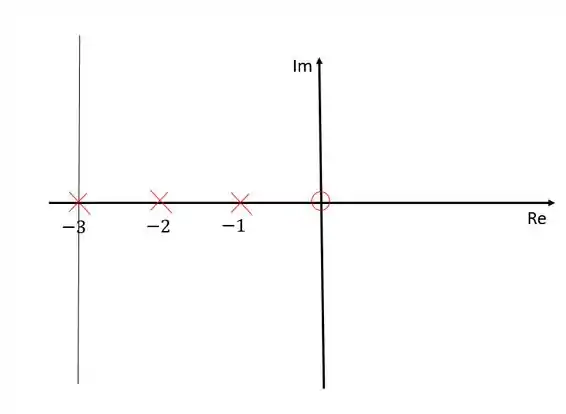
Agora vamos calcular onde a assíntota intercepta o eixo real:
Coocando no diagrama de lugar das raízes:
Passo 3
Só precisamos agora representar os ramos do lugar das raízes seguindo todas aquelas regrinhas. Os ramos nascem nos polos e morrem nos zeros. O número de ramos é igual ao número de polos, e os ramos só existem se à esquerda deles existir um número ímpar de polos e zeros.
Portanto:
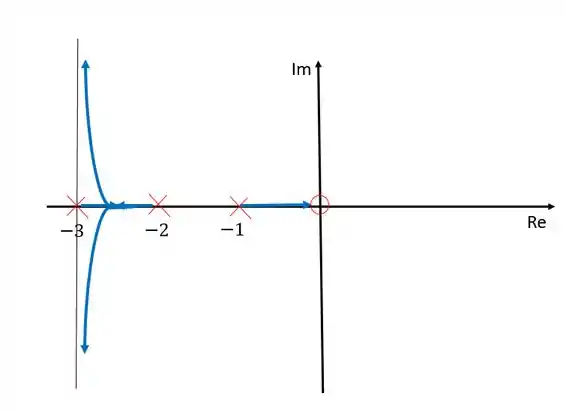
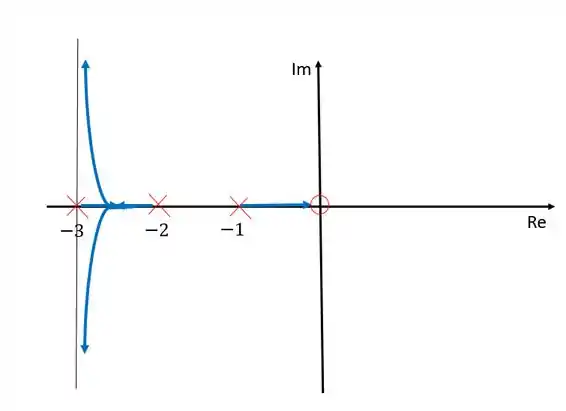
Nesse caso nós temos três ramos pois temos três polos. Entre e não pode haver nenhum ramo pois existe uma uantidade par de polos e zeros à esquerda desse trecho. Como temos dois polos a mais que zeros, dois ramos morrerão no infinito. Esses ramos saem de e , se encontram no meio desse trecho e depois tendem assintoticamente aos zeros determinados pelas assíntotas calculadas.
Resposta