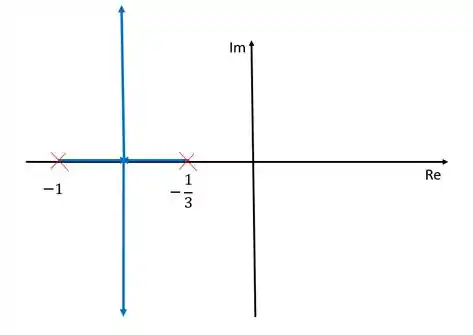
Esboce o lugar geométrico das raízes e suas assíntotas para o sistema mostrado abaixo:
Passo 1
Como sempre, a primeira coisa que devemos começar fazendo é identificar quantos e quais são os polos e zeros da função de transferência.
Para este caso, nós não temos nenhum zero na função de transferência, porém temos dois polos, e . Vamos marcar eles no diagrama então:
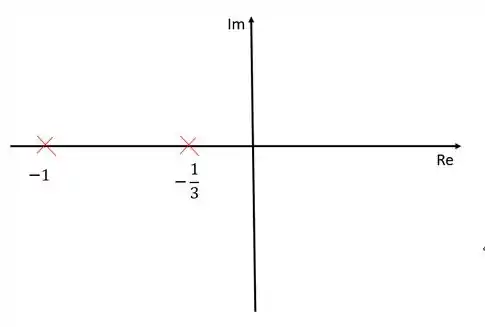
Passo 2
Como temos dois polos a mais que zeros, isso indica que teremos dois zeros no infinito no nosso diagrama. Para saber a localização desses zeros desenharemos assíntotas no diagarama de lugar das raízes que vão nos indicar onde eles se encontram.
Podemos perceber que se for igual a o ângulo será , se for , será . Após isso, os valores e começam a se repetir.
Agora vamos calcular onde a assíntota intercepta o eixo real:
Coocando no diagrama de lugar das raízes:
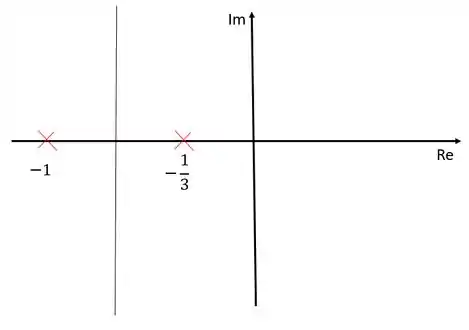
Repare que temos duas assíntotas, uma com inclinação e outra com inclinação .
Passo 3
Por fim devemos representar os ramos, eu são as linhas eu indicam o lugar das raízes conforme varíamos algum coeficiente (nesse caso, o ganho). Lembre-se sempre que o número de ramos é sempre igual ao númeor de polos e que cada ramos “nasce” em um polo e “morre” em um zero. Então nesse caso nós teremos um ramo saindo de cada um dos polos e indo até um zero no infinito pois não temos nenhum zero finito.
Outro detalhe importante é que os ramos só existem no eixo dos reais se estiverem à esquerda de um número ímpar de polos, ou seja, não pode existir nenhum ramo à direita de pois nesse caso não teríamos nenhum polo à esquerda, nem à esquerda de pois aí teríamos dois polos à esquerda.
Sendo assim, o nosso diagram de lugar das raízes fica da seguinte forma:
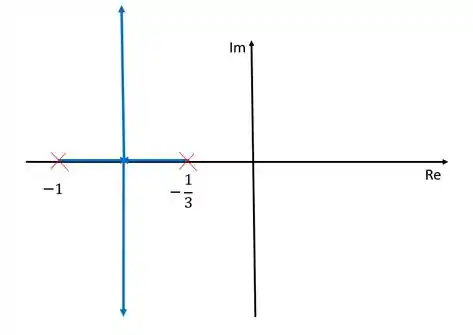
Nesse caso, coincidentemente, o ramo do lugar das raízes ficou sobre as assíntotas, mas tenha em mente que nem sempre será assim.
Resposta