Esboce o lugar geométrico das raízes e suas assíntotas para o sistema mostrado abaixo:
Passo 1
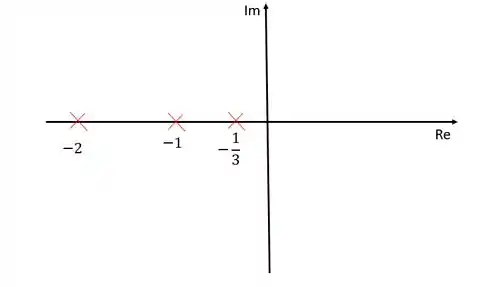
Primeiramente vamos identificar nosso polos e zeros. Nesse caso, temos três polos, , e , e nenhum zero.
Representando esses polos no diagrama de lugar das raízes:
Passo 2
Nesse caso, temos três polos a mais que zeros, isso indica que teremos três zeros no infinito, e portanto, precisamos das nossas assíntotas para saber a localização desses polos.
Podemos perceber que se for igual a o ângulo será , se for , será , e será se for . Após isso, os valores começam a se repetir.
Agora vamos calcular onde a assíntota intercepta o eixo real:
Colocando no diagrama de lugar das raízes:
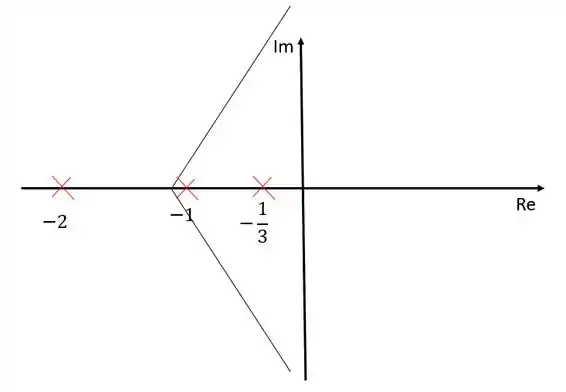
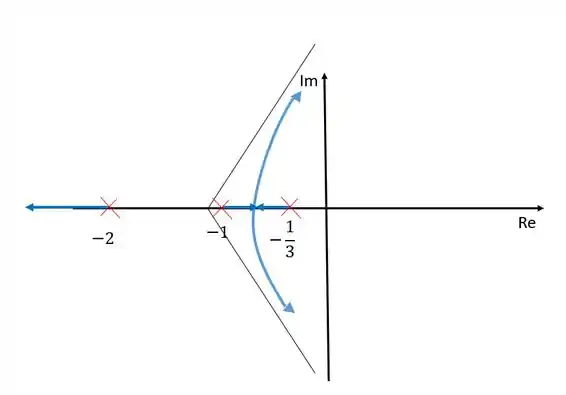
Temos uma assíntota com inclinação , uma assíntota com inclinação e uma terceira assíntota com inclinação que se encontra sobre o eixo dos reais.
Passo 3
Agora só nos resta representar os ramos, lembrando sempre das nossas regrinhas: os ramos nascem nos polos e morrem nos zeros, o número de ramos é igual ao número de polos, e os ramos só existem se à esquerda deles existir um número ímpar de polos e zeros.
Se observarmos todas essas regras, nosso diagram ficará dessa forma:
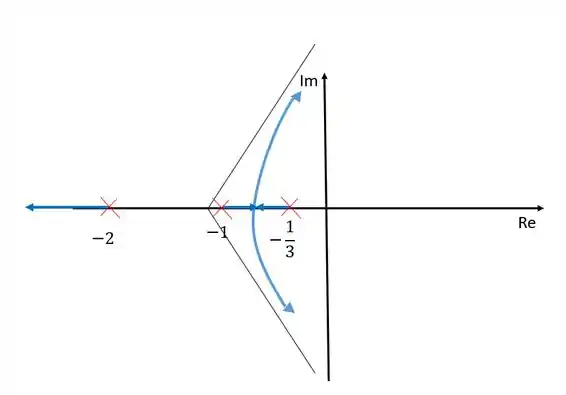
Cada ramo nasce em um polo e morre em um zero no infinito, já que não temos nenhum zero finito nesse caso. Os zeros no infinito são determinados pelas assíntotas e portanto os ramos tendem à eles.
Entre e não existem ramos porque nesse intervalo existem dois polos à esquerda.
Resposta