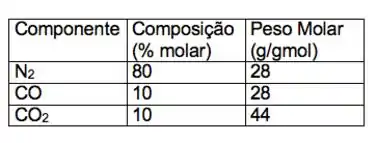
Calcule a densidade do ar atmosférico seco à e .Considere-o como gás ideal e com a seguinte composição:
Passo 1
Coloca uma estrelinha nesse exercício, ok? Como o enunciado diz pra considerar gás ideal, vale a equação dos gases ideais:
Em que:
O enunciado já deu que
E deu a temperatura também, mas em graus Celsius, que não é uma escala absoluta.
As escalas absolutas de temperatura são Kelvin e Rankine. Vou escolher converter essa temperatura para Kelvin então:
Posso cortar as denominadores porque são iguais
A temperatura em , que chamei de , vale . Jogando na fórmula, achamos a temperatura em Kelvin, que chamei de :
Ou seja:
Só uma coisa sobre nomenclatura: falamos só “Kelvin” e NÃO graus Kelvin, ok?
Temos agora que manipular o e fazer a densidade aparecer.
Passo 2
Bora lá. Vamos olhar a definição de , que é o número de moles:
Mas o ar atmosférico é uma mistura e não uma substância pura. Daí, para calcular o número de moles de uma mistura, usamos a massa da mistura e a massa molecular média da mistura:
Repara que eu coloquei uma barrinha em cima de . Usamos essa barrinha pra representar valor médio.
Substituindo isso na equação dos gases ideiasE agora, a rearranjando:
Isolei o . E o que é isso? A densidade! Show então.
Passo 3
Ok. Mas até agora não calculamos a e vamos precisar dela. Então bora acabar logo com isso e calcular haha.
Temos pesos moleculares (= massa molar) de cada um dos componentes puros e a porcentagem de cada um deles no ar seco. Daí, temos que fazer uma média ponderada.
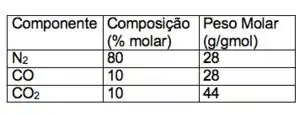
Posso dividir logo as porcentagens pelo 100, tipo assim olha:
Daí:
Não podemos nos esquecer da unidade:
Passo 4
Agora, só falta um detalhe antes de calcular a densidade: qual o valor de ?
Provavelmente você já sabe que tem um milhão de valores tabelados para , com diferentes unidades. Vamos ver se com as unidades que estamos usando para , , e , tem algum tabelado que possamos usar direto. Caso contrário, teremos que converter unidades.
Opa! Dá uma olhada nesse daqui:
Per-fei-to! Nossa já está em , a em e a em .
Daí, usando esse , a densidade sai em . Saca só:
Fazendo análise dimensional:
Esses colchetes significam a unidade do que está dentro deles.
Cortando tudo que dá pra cortar:
Passo 5
Chegou, finalmente, a hora de substituir todos os valores pra calcular essa densidade aí:
Pronto! Achamos! Como o enunciado não especificou unidade pra densidade, podemos deixar assim mesmo.