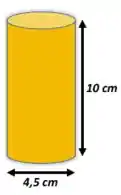
Calcule a massa do cilindro de ouro abaixo, sabendo que a densidade do ouro é .
Passo 1
Essa questão é quase uma aplicação direta da fórmula da densidade.
O enunciado deu a densidade do ouro
Deu também as dimensões do cilindro:
Então podemos calcular o volume dele.
Depois, é só lembrar que a definição de densidade é:
E calcular a massa : )
Passo 2
A nossa “partícula” é o cilindro. Então vamos começar calculando o volume desse cara:
Substituindo os valores:
Mas repara que o volume na densidade que temos está em e não em , então, bora converter esse volume do cilindro aí:
Daí:
Cortamos os e aí:
Passo 3
Agora que já temos o volume do cilindro, é só aplicar a definição de densidade e calcular a massa: