Deformações Inelásticas e Tensões Residuais
Teoria
Nesse tópico, vamos aprender sobre deformações plásticas (ou inelásticas) e sobre como elas podem levar ao surgirmento de tensões residuais em uma peça.
Não são todos os professores que ensinam e cobram esse assunto. Se esse assunto não fizer parte da sua prova, sinta-se livre para pular ele! ⚠
Introdução
Vamos dizer que a nossa empresa de consultoria em projeto de estruturas, a Dexter Structures, foi contratada para avaliar a seguinte estrutura:
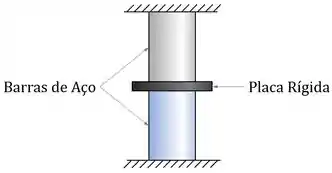
Nessa estrutura, as duas barras de aço tem o mesmo módulo de elasticidade , o mesmo comprimento e a mesma área de seção transversal .
Mas elas têm uma diferença: A barra de cima tem uma tensão de escoamento , enquanto que a barra de baixo tem uma tensão de escoamento .
O motivo é que a barra de cima foi comprada de um fornecedor confiável, enquanto que a barra de baixo é de origem duvidosa:
Deformações Elástica e Plástica
Agora, vamos aplicar uma força para baixo na placa rígida.
Por causa dessa força , as barras vão se deformar: a barra de baixo vai ser comprimida e a barra de cima vai ser esticada:
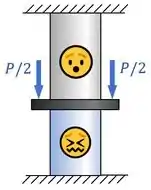
Enquanto que as tensões nas barras forem menores que as tensões de escoamento de cada uma, as barras vão se comportar elasticamente.
Ou seja, as deformações nas barras vão ser lásticas (e reversíveis!) e as fórmulas da Lei de Hooke e da variação de comprimento vão estar valendo.
Mas...
Se o carregamento for grande demais, a tensão na barra de baixo pode atingir a tensão de escoamento .
Nesse caso, a barra de baixo vai escoar: ela vai deixar de se comportar elasticamente e vai começar a se comportar plasticamente.
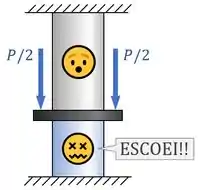
A partir desse momento, qualquer deformação a mais que a barra sofrer vai ser uma deformação lástica ou inelástica , que é uma deformação permanente.
Tensões Residuais
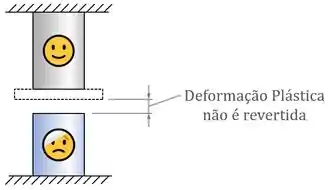
Agora, o que é que acontece se, depois da nossa barra de baixo ter sofrido uma deformação permanente, nós tirarmos o carregamento ?
As barras vão querer voltar para os seus tamanhos originais!!
A barra de cima, que só sofreu deformação elástica/reversível, conseguiria reverter essa deformação facilmente.
Já a barra de baixo, que foi “machucada” com um pouco de deformação permanente, só conseguiria reverter a parte elástica da deformação que ela sofreu:
Mas a verdade é que essa situação da imagem acima é só como as barras gostariam de estar.
Na realidade, como elas têm que estarem conectadas entre si, elas vão acabar se tracionando mutuamente para que elas possam se “encontrar”:
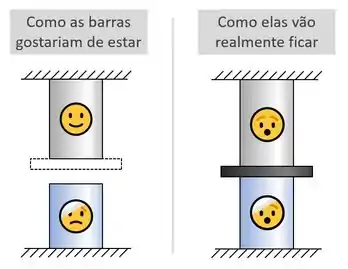
Essa tração mutua vai então gerar uma tensão nas barras.
Mas essa tensão não vai estar vindo de nenhum carregamento externo. Ela vai ser tipo uma tensão fantasma que vem do próprio sistema.
Essas tensões fastasmas são o que a gente chama de tensões residuais.
Beleza! Mas eu tenho uma dúvida...
Quando é que tensões residuais acontecem?
Em outras palavras, em que outras situações eu tenho que me preocupar com elas?
Então! A boa notícia é que elas só acontecem em condições específicas, que são:
1. Você tem uma ou mais peças que estão estaticamente indeterminadas;
2. Essas peças são carregadas (ou mecanicamente, através de uma força, ou termicamente, através de uma variação de temperatura);
3. Esse carregamento é tão grande que uma das peças sofre uma deformação plástica/permanente;
4. E, após essa deformação permanente, as peças são descarregadas.
Então, você pode observar que em qualquer exercício de tensão residual, essas quatro condições vão estar acontecendo nessa ordem.
Tá... Mas eu tenho outra dúvida...
Como é que eu calculo as tensões residuais em uma peça?
Vamos ver isso agora!!
Cálculo de Tensões Residuais
Aqui na Dexter Structures nós somos práticos, então eu já vou te passar direto o bizu de calcular tensões residuais.
Primeiro eu vou te passar o método tradicional, dos livros, em quatro passos.
Depois vou passar a fórmula da tensão residual, um método acelerado, mas que infelizmente não é aceito por 100% dos professores. (Verifique se você pode usá-la!)
Método Tradicional
1. O primeiro passo é calcular as tensões nas peças fingindo que elas só se comportam elasticamente.
Como todo exercício de tensão residual é estaticamente indeterminado, você vai ter que usar equações de equilíbrio & equações de compatibilidade para encontrar essas tensões.
Aqui nesse primeiro passo, você está livre para usar as fórmulas de sempre como (Lei de Hooke) e (Variação de Comprimento Elástica).
2. Em seguida, você vai verificar se a tensão encontrada para alguma peça tem uma intensidade maior que a tensão de escoamento da peça.
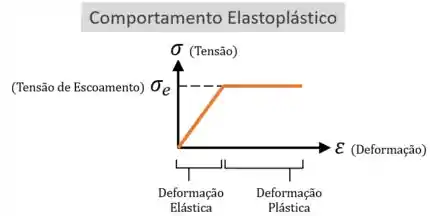
Se isso acontecer, aí você vai ter que considerar que a peça tem um comportamento elastoplástico (ou “elástico perfeitamente plástico”).
Isso significa dizer que...
Uma vez que a tensão na peça atingiu o limite , ela passou a se deformar plasticamente de forma livre, sem haver qualquer aumento correspondente de tensão:
Dessa forma, você vai:
- Dizer que a tensão calculada é impossível;
- Definir um novo valor para , com a mesma intensidade da tensão de escoamento ;
- E inserir esse novo valor na fórmula para encontrar os novos valores correspondentes da força normal e das reações nas peças.
Rola sim!
Vamos dizer que a gente encontrou no Passo 1 que a tensão na barra de baixo do nosso exemplo é .
Essa tensão tem uma intensidade maior que a tensão de escoamento da barra.
Então vamos dizer que essa tensão de é impossível e que o novo valor de , igual à tensão que realmente aconteceu, é .
Em seguida, pegamos esse novo valor de e inserimos na fórmula da tensão normal média .
Com isso, vamos conseguir definir um novo valor para a força normal na nossa barra.
E como a força normal pode ser descrita em função das forças de reação que o solo e o teto fazem nas barras, conseguimos também definir novos valores para essas reações.
E, se preciso, conseguimos definir também novos valores para as tensões em outras peças.
3. O terceiro passo é encontrar a variação de comprimento plástica sofrida pela peça que atingiu sua tensão de escoamento.
Para fazer isso, você vai pegar a sua equação de compatibilidade do Passo 1 e:
- Chamar as variações de comprimento antigas que seguiam o comportamento elástico de variações elásticas ;
- E adicionar a variação de comprimento plástica ,
Como mostram os exemplos abaixo:
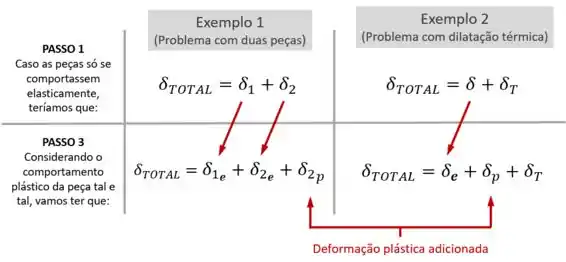
Aí, isolando a variação de comprimento plástica na nova equação de compatibilidade, você consegue encontrar ela.
Aqui, você só deve tomar o cuidado de re-calcular as variações de comprimento elásticas usando os novos valores das tensões , das forças normais e das reações nas peças.
4. O último passo é calcular as tensões na situação final, depois que a peça foi descarregada.
Ou seja, você vai tirar o carregamento que existia na peça e refazer o Passo 1, usando equações de equilíbrio & equações de compatibilidade para determinar as tensões na peça.
Aí, como a variação de comprimento plástica encontrada no passo anterior é permanente, ela deve fazer parte da equação de compatibilidade nessa situação final.
Finalmente, as tensões que você encontrar aqui vão ser as tensões residuais nas peças.
Fórmula da Tensão Residual
Olhando para esse método tradicional de resolução de exercícios de tensão residual, ele parece bem longo, né?
Então, eu vou te passar agora o segredo industrial da Dexter Structures! 🐵
Sabe como no Passo 1, a gente encontrou as tensões que aconteceriam caso as peças só se comportassem elasticamente?
Vamos chamar as tensões nessa situação hipotética de .
E sabe como no Passo 2, a gente definiu as tensões reais que realmente aconteceram?
Então... A tensão residual em uma peça é a diferença entre a tensão real e a tensão hipotética :
Simples assim? 🤔
Sim!!! Simples assim! 😍
Então eu posso só fazer o Passo 1 e parte do Passo 2 e depois aplicar essa fórmula aí?
Sim!!
O único cuidado que você deve tomar é o de usar os sinais corretos de tensão (positivo para tração e negativo para compressão) tanto para a tensão real quanto para a hipotética .
Fazendo isso, o resultado para a tensão residual vai sair bonitinho, com sinal correto e tudo.
PS: Fica o convite para você treinar o que aprendeu e ficar craque fazendo uns exercícios resolvidos!
Primeiro tem uns exercícios para treinar os conceitos básicos de deformação plástica/inelástica e depois tem uns de tensão residual mesmo para você tirar aquele notão.
Tensões Residuais
Cálculo de Tensões Residuais
Fórmula da Tensão Residual
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria.
O comportamento da barra de alumínio abaixo pode ser considerado elastoplástico com e . Determine qual é a força necessária para fazer essa barra começar a se deformar plasticamente.
As áreas das seções transversais dos trechos e da barra são fornecidas na imagem.
Passo 1
O que está acontecendo?
As forças de tração geram ao longo de toda a barra uma força interna normal .
Essa força normal gera, nos trechos e da barra, tensões normais médias :
Onde e são as áreas das seções transversais dos trechos e da barra.
Para que a barra se deforme plasticamente, só é necessário que um dos seus trechos se deforme plasticamente.
E para que um trecho da barra se deforme plasticamente, é necessário que a tensão normal nesse trecho alcance o limite de resistência ao escoamento do material.
Para uma mesma força , o trecho que irá atingir essa tensão primeiro vai ser o trecho com a menor área de seção transversal . (No nosso caso, o trecho !)
E o que é que o exercício quer?
Ele quer saber qual é a força necessária para fazer a barra se deformar plasticamente.
(Ou seja, a força necessária para fazer um dos trechos da barra se deformar plasticamente.)
Passo 2
Então vamos lá!
A barra vai se deformar plasticamente primeiro no trecho , que possui uma área de seção transversal menor.
Então a força necessária para fazer a barra se deformar plasticamente é a força que faz com que a tensão em , , seja igual à tensão de escoamento :
Aplicando a fórmula da tensão normal média para o trecho , vamos ter:
Como a única força atuante na barra é a tração , a força interna normal na barra vai ser igual à .
Dessa forma, temos que:
Isolando , temos:
Substituindo os valores:
- ;
- & ,
Vamos encontrar que:
Como esse número é um pouco grande, podemos reescrevê-lo em :
Ou seja, precisamos de uma força para fazer a barra começar a se deformar plasticamente!
Resposta
Exercício Resolvido #2
Elaboração Própria.
A prensa hidráulica abaixo é utilizada para comprimir o corpo de prova, que possui uma área de seção transversal , um comprimento inicial e um comportamento elastoplástico com e .
Se a prensa causa no corpo de prova uma variação de comprimento máxima , determine quais foram as variações de comprimento elástica e plástica sofridas pelo corpo de prova.
Passo 1
O que está acontecendo?
O corpo de prova se comporta de forma elastoplástica com um módulo de elasticidade e um limite de resistência ao escoamento .
Além disso, ele tem um comprimento inicial .
A prensa hidráulica vai comprimir esse corpo de prova, gerando nele uma variação de comprimento máxima .
Essa variação de comprimento máxima é composta por:
- Uma variação de comprimento elástica , que segue a Lei de Hooke, e ocorre até que a tensão no material alcance a tensão de escoamento ;
- E uma variação de comprimento plástica , que ocorre depois da tensão no material ter alcançado .
Ou seja, caso a tensão no material alcance , a variação de comprimento máxima vai ser:
E o que é que o exercício quer?
Ele quer que a gente calcule os valores de e .
Primeiro, devemos calcular o valor máximo da variação de comprimento elástica , que é o valor que ocorre quando a tensão no material é igual à .
Se essa variação elástica máxima for maior ou igual à variação de comprimento máxima no material, então toda a variação sofrida vai ter sido elástica.
Mas se essa variação elástica máxima for menor que , então a diferença será a variação de comprimento plástica .
Passo 2
Vamos começar calculando o valor máximo possível para !
O valor máximo da variação de comprimento elástica é aquele que ocorre quando a tensão no material é igual à , então vamos aplicar essa condição:
Mas, da Lei de Hooke, temos que , onde é a deformação elástica sofrida pelo material. Então:
Se é a deformação elástica sofrida pelo material, então é igual à variação de comprimento elástica sofrida dividida pelo comprimento da peça:
Assim, encontramos que:
Substituindo os valores:
- ;
- ;
- & ,
Encontramos que:
Passo 3
Agora vamos pensar...
Encontramos que o valor máximo possível para é , o que é muito menor que a variação de comprimento máxima sofrida pelo nosso corpo de prova.
Então o que aconteceu foi que:
- A tensão de escoamento foi atingida na peça;
- Por causa disso, a peça sofreu uma variação de comprimento elástica ;
- E também por causa disso, a peça começou a se comportar plasticamente, o que significa que todo o restante da variação de comprimento sofrida foi plástica.
Sabendo disso, já podemos calcular a variação de comprimento plástica na peça:
Substituindo e , encontramos que:
E assim finalizamos nosso exercício!
Resposta
Exercício Resolvido #3
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 138-2.105.
A barra consiste em duas partes cilíndricas e ; ela é feita de um aço doce considerado elastoplástico com e . Uma força é aplicada à barra e em seguida removida para dar a ela uma deformação permanente . Determine o valor máximo da força e o valor máximo de pelo qual a barra deverá ser alongada para dar a ela a deformação permanente desejada.
Passo 1
O que está acontecendo?
A barra é feita de dois segmentos:
- Um segmento de diâmetro e comprimento ;
- E outro de diâmetro e comprimento .
Além disso, ela possui um comportamento considerado elastoplástico com módulo de elasticidade e tensão de escoamento .
O que isso significa é que quando a tensão é atingida na barra, ela não é capaz de resistir qualquer tensão maior e passa a se deformar plasticamente/permanentemente.
No caso da nossa barra, a tensão vai ser atingida primeiro no trecho , que possui um diâmetro menor, e, consequentemente, uma área de seção transversal menor.
Isso significa que a variação de comprimento nesse trecho vai ser a soma:
- De uma variação de comprimento elástica até que a tensão de escoamento fosse atingida;
- Com uma deformação plástica/permanente que ocorre depois que a tensão de escoamento foi atingida.
Ou seja:
Já a variação de comprimento sofrida pelo trecho vai ser puramente elástica, uma vez que a tensão de escoamento nunca vai ser atingida nesse trecho.
(O trecho vai começar a se deformar livremente impedindo o aumento da carga e das tensões em toda a peça assim que a tensão nele alcançar .)
Então vamos ter que:
Então como o segmento não sofre deformação permanente, podemos dizer que toda a deformação permanente sofrida pela barra foi sofrida pelo segmento .
Ou seja:
E o que é que o exercício quer?
Primeiro, ele quer saber o valor máximo da força que foi aplicada nessa barra para que ela sofresse essa deformação plástica.
Como é o trecho que sofre a deformação plástica, o valor máximo de vai ser o valor para o qual a tensão normal média no trecho é igual à tensão de escoamento :
(Isso porque quando essa condição é atingida, a barra passa a se deformar livremente, impedindo que a força seja aumentada.)
Depois, ele quer saber a variação de comprimento máxima que foi sofrida pela barra para que ela tivesse a deformação permanente no trecho .
Aqui, podemos perceber que a variação de comprimento máxima da barra vai ser a soma das variações de comprimento de cada segmento:
Substituindo as expressões que encontramos para e , temos que:
Nessa expressão, sabemos que e que uma variação de comprimento pode ser calculada pela fórmula se ela for elástica.
Passo 2
Então para encontrar a força máxima na barra, vamos aplicar a condição de que ela acontece quando:
Aplicando a fórmula da tensão normal média para o trecho , temos que:
Como o único carregamento na barra é a tração , a força interna normal vai ser igual à , tanto no trecho quanto no trecho .
Além disso, o trecho possui uma seção transversal circular de diâmetro .
Então a área dessa seção transversal pode ser calculada usando a fórmula .
Aplicando tudo isso, a nossa expressão anterior fica assim:
Queremos encontrar a força máxima , então devemos isolá-la:
Finalmente, substituindo os valores:
- ;
- & ,
Encontramos que:
Como esse número é um pouco grande, podemos reescrevê-lo em na hora de darmos a nossa resposta para a primeira parte do exercício:
Passo 3
Agora, na segunda parte do exercício, queremos encontrar a variação de comprimento máxima que foi sofrida pela barra.
Como vimos no Passo 1, essa variação vai ser a soma:
- Das variações de comprimento elástica dos segmentos e ;
- Com a variação de comprimento permanente/plástica que foi sofrida pelo segmento .
Ou seja:
Nessa expressão, podemos desenvolver as variações elásticas usando a fórmula .
Aplicando essa fórmula para e para , vamos ter que:
Mais uma vez, como o único carregamento na barra é a tração , a força interna normal vai ser igual à , tanto no trecho quanto no trecho .
Além disso, como as áreas e são circulares, elas podem ser fornecidas em função de seus diâmetros e usando a fórmula .
Aplicando tudo isso, a expressão anterior fica assim:
Arrumando tudo, temos:
Colocando em evidência, temos:
Finalmente, substituindo os valores:
- ;
- ;
- e ;
- e ;
- & ,
Encontramos que:
Que é a nossa resposta para a segunda e última parte o exercício!
Resposta
Exercício Resolvido #4
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 139-2.116.
Uma barra de aço uniforme de seção transversal com área é ligada a suportes rígidos e está livre de tensões a uma temperatura de . O aço é considerado elastoplástico com e . Sabendo que , determine a tensão na barra quando a temperatura for elevada a e depois que a temperatura retorna a .
Passo 1
A barra tem uma área de seção transversal e um comprimento .
A uma temperatura inicial , a barra está livre de tensões.
E ela é feita de um aço elastoplástico com resistência ao escoamento , módulo de elasticidade e coeficiente de dilatação térmica .
Beleza, e o que é que está acontecendo?
No item a temperatura na barra é elevada até uma temperatura final , sofrendo então uma variação de temperatura:
Por causa dessa variação de temperatura, a barra vai sofrer uma deformação térmica :
(Como o comprimento da nossa barra é desconhecido, é mais prático trabalhar com do que trabalhar com a dilatação térmica .)
Agora, essa barra é ligada a suportes rígidos dos dois lados que não permitem com que a barra se deforme livremente.
Esses suportes rígidos requerem que a deformação total da barra seja igual à zero:
Para fazer com que isso aconteça, eles realizam forças de reação na barra:
Essas forças compressivas geram na barra:
- Uma força interna normal ;
- Uma tensão normal média ;
- E, de acordo com a Lei de Hooke (), uma .
Daí que pelo princípio da superposição, a deformação total na barra vai ser a soma da deformação térmica com a deformação causada pelas forças :
Daí que podemos usar essa fórmula acima para encontrar qual vai ser o valor da tensão normal média que vai surgir na nossa barra.
Mas calma aí...
O nosso material é elastoplástico. Então a tensão máxima que pode ser alcançada nele é a tensão de escoamento .
Daí que se encontrarmos que a tensão normal média que deveria surgir na nossa barra é maior que , na realidade o que vai acontecer é que:
1. A tensão que vai surgir vai ser a tensão máxima ;
2. O material vai começar a escoar/a se deformar plasticamente;
E assim, 3. A deformação causada pelas forças vai passar a ser a soma:
- De uma deformação elástica (correspondente à tensão máxima de acordo com a Lei de Hooke);
- Com uma deformação plástica .
Dessa forma, a variação de comprimento total vai ser escrita assim:
E o que é que o exercício quer?
No item , ele quer saber qual vai ser a tensão gerada na barra.
Devemos calcular essa tensão usando a relação .
Mas se o valor final encontrado for maior que , a tensão gerada vai ser .
E nesse caso, vamos poder calcular também a deformação plástica sofrida pela barra.
O que é interessante porque...
No item , ele quer saber qual vai ser a tensão na barra quando a temperatura voltar para .
A princípio, essa tensão seria nula. Mas se o material tiver sofrido uma deformação plástica , essa deformação vai ter sido permanente.
Dessa forma, os suportes rígidos da barra vão ter que realizar forças na barra para gerar nela:
- Uma tensão normal ;
- E, de acordo com a Lei de Hooke, uma deformação .
- ;
- ;
- & ,
- ;
- ;
- & ,
- O valor da variação de comprimento total , que deve ser igual à ;
- A fórmula da deformação térmica ;
- & a deformação elástica de acordo com a Lei de Hooke, tendo em mente que a tensão efetivamente gerada na barra é ,
- Uma tensão normal ;
- E, de acordo com a Lei de Hooke, uma deformação .
Essa deformação , superposta com a deformação permanente , vai conseguir garantir com que a deformação total da barra continue nula:
Passo 2
É muita coisa, mas vamos lá, a gente consegue! 👊
Primeiro, vamos calcular a tensão na barra quando a temperatura é elevada usando a relação:
Substituindo:
Isso fica assim:
Isolando , encontramos:
Finalmente, substituindo os valores...
...encontramos que:
Mas esse valor é impossível pois ele ultrapassa a intensidade da tensão de escoamento .
Então temos que a nossa resposta para o item , a tensão que vai ser efetivamente gerada na barra vai ser:
Passo 3
Em seguida, vamos definir a deformação plástica sofrida pela barra.
Para tanto, aplicamos a relação:
Substituindo:
A relação acima fica assim:
Isolando a deformação plástica , temos:
Não precisamos calcular a deformação plástica em si, então vamos só guardar essa expressão.
Passo 4
Agora, na situação do item , vamos ter deformação plástica , que por ser permanente, permaneceu mesmo após a volta da temperatura para .
Por causa disso, os suportes rígidos da barra vão ter que realizar forças na barra para gerar nela:
Dessa forma, a deformação total na barra vai ser:
Substituindo:
- ;
- A expressão encontrada para ;
- & ,
Isso fica assim:
Queremos encontrar a tensão nessa nova situação, então devemos isolá-la:
Simplificando tudo, isso fica assim:
Por fim, substituindo os valores...
- ;
- ;
- ;
- & ,
...encontramos que:
Que é a nossa resposta do item !
Resposta
Exercício Resolvido #5
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 120-4.99.
A barra tem área de seção transversal de . Se uma força for aplicada em e, então, removida, determine a tensão residual nas seções e .
Dados: .
Passo 1
O que está acontecendo?
A barra tem uma área de seção transversal e é feita de um material com um limite de resistência ao escoamento .
Ela é dividida nos trechos , de comprimento , e , de comprimento por uma força .
E ela é apoiada por forças de reação e nos apoios em e em , como mostra o seu diagrama de corpo livre:
Como esses apoios em e em são fixos, eles garantem que a variação de comprimento total na barra seja sempre igual à zero:
E o que é que o exercício quer?
Ele quer saber a tensão residual nas seções e da barra quando a força é retirada.
Para que essa tensão residual exista, é necessário que o carregamento original da barra tenha gerado nela alguma variação de comprimento plástica/permanente .
Então vamos:
1. Analisar a barra em sua situação inicial para descobrirmos se vai haver alguma variação de comprimento permanente nela.
Para tanto, devemos:
- Considerar que não vai haver deformação plástica;
- E calcular as tensões nos trechos e da barra, verificando se elas vão ultrapassar ou não a resistência ao escoamento .
Se a tensão em um trecho ultrapassar , então vai haver deformação plástica.
Nesse caso, vamos ter que:
2. Adicionar a deformação plástica à nossa análise e definir .
E, por último, vamos:
3. Analisar a barra em sua situação final para descobrirmos qual é a tensão residual correspondente à variação de comprimento plástica gerada.
Passo 2
Então vamos começar avaliando a barra considerando que não vai haver deformação plástica.
Primeiro, observando o diagrama de corpo livre da barra...
...e aplicando o equilíbrio de forças na vertical:
...encontramos que:
Em seguida, fazendo uma análise dos esforços internos na barra, vamos ter que:
Para as seções entre e ...
...o equilíbrio de forças requer que:
Mas como , isso significa que:
Já para as seções entre e ...
...o equilíbrio de forças requer que:
Por fim, a última análise que podemos fazer é encontrar uma equação de compatibilidade para a barra.
Por um lado, temos que a variação de comprimento total da barra deve ser igual à zero por causa dos apoios fixos:
Do outro, temos que a variação de comprimento total da barra é a soma das variações de comprimento dos trechos e .
Dessa forma, temos que:
Agora, como estamos considerando que não vai haver deformação plástica, podemos dizer que essas variações de comprimento e podem ser dadas pela fórmula:
Aplicando essa fórmula para e , a nossa equação de compatibilidade fica assim:
Multiplicando tudo por , temos que:
Em seguida, substituindo...
- Os comprimentos e ;
- & as forças normais e ,
...temos que:
Multiplicando tudo por , isso fica assim:
Fazendo as multiplicações, temos que:
E, finalmente, isolando , encontramos que:
E como , isso significa que:
Passo 3
Já analisamos toda a barra considerando que não vai haver deformação plástica.
Então agora podemos calcular quais seriam as tensões nos trechos e nesse caso.
Aplicando a fórmula da tensão normal média para o trecho , temos:
Substituindo , isso fica assim:
Em seguida, substituindo...
- ;
- ;
- & ,
...e prestando atenção nas unidades, encontramos que:
O que é menor que a tensão de escoamento .
Ou seja, o trecho da barra não vai sofrer deformação plástica.
Já aplicando a fórmula da tensão normal média para o trecho , temos:
Substituindo , temos:
E em seguida, substituindo e , encontramos que:
Vemos que a intensidade de é maior que a tensão de escoamento .
Então o trecho vai sofrer deformação plástica e a tensão que vai ocorrer efetivamente nele vai ser .
Isso significa que a força também não vai chegar a ser igual à .
Pegando a expressão:
Isolando :
E substituindo e , encontramos que efetivamente, o valor de vai ser:
Dica: Na hora da prova, destaque esses novos valores com uma caixa “novos valores” ou algo parecido. Assim você não se esquece deles!
Passo 4
Agora que sabemos que o trecho vai sofrer deformação plástica, podemos adicionar essa informação à nossa análise.
A equação de compatibilidade que antes era assim...
...agora vai levar em consideração que:
- A variação de comprimento do trecho só tem uma parcela elástica ;
- E que a variação de comprimento de tem uma parcela elástica e uma parcela plástica .
Dessa forma, a equação de compatibilidade vai ficar assim:
Aqui, como as variações de comprimento e são elásticas, podemos aplicar a fórmula para elas:
Substituindo essas expressões, a equação de compatibilidade fica assim:
Isolando , temos:
Substituindo , , e isso fica assim:
Colocando em evidência, temos:
E, finalmente, simplificando, isso fica assim:
Não precisamos realmente calcular , então vamos só guardar essa expressão para depois.
Passo 5
Agora que já sabemos que a peça vai sofrer uma deformação plástica , podemos ver que tensão residual essa deformação plástica vai gerar depois que a força for retirada.
Quando a força for retirada, o diagrama de corpo livre da barra vai ficar assim:
Essas reações só existem para compensar a deformação plástica e garantir que a variação de comprimento total na barra seja igual à zero.
Elas fazem isso gerando, ao longo de toda a barra:
- Uma força interna normal , e, consequentemente, uma tensão normal média ;
- E uma variação de comprimento .
Superpondo a variação de comprimento plástica com essa variação de comprimento causada pelas reações , temos a variação de comprimento total:
Impondo a condição , isso significa que:
Substituindo e a expressão encontrada no passo anterior para , temos:
Cortando com e com , encontramos a tensão residual que vai aparecer ao longo de toda a barra por causa da deformação plástica ocorrida:
Finalmente, substituindo...
- ;
- O novo valor encontrado para no Passo 3, ;
- & ,
...encontramos que a tensão residual ao longo de toda a barra (ou seja, tanto no trecho quando no trecho ) vai ser:
Como esse número é muito pequeno, podemos reescrevê-lo em na hora de fornecermos a nossa resposta:
Resposta
Exercício Resolvido #6
Elaboração própria
Verifique se o problema abaixo apresenta tensões residuais. Caso apresente determine o valor delas.
Passo 1
Sabemos que para sabermos quais tensões agem na nossa peça, precisamos determinar os normais que estão agindo nela, faremos esse exercício das duas formas que aprendemos, primeiro pelo método mais longo, e depois conferiremos a reposta pelo método mais curto.
Sabemos que o método mais longo passa por 4 etapas que são
Primeiro calcularemos as tensões na peça fingindo que ela se comporta elasticamente.
Em segundo conferimos se em algum ponto da peça a tensão calculada é maior que a tensão de escoamento, e caso seja modificamos a nossa conta.
Em terceiro lugar calculamos as deformações plásticas.
E por fim calculamos as tensões residuais.
Para o método mais rápido sabemos que apenas os passos 1 e 2 já resolvem o nosso problema. Mas antes de fazermos essa analise precisamos conhecer os esforços na barra.
Passo 2
Como podemos ver, nesse tipo de questão precisamos determinar as reações de apoio. Para determinarmos essas reações de apoio precisamos saber se o nosso problema é isostático ou se é um problema estaticamente indeterminado. Como temos duas paredes no nosso problema, podemos desconfiar que talvez seja a segunda opção.
Para termos certeza que se trata de um problema estaticamente indeterminado, precisamos definir o diagrama de corpo livre e fazer o balanceamento entre o número de incógnitas e o número de equações, então vamos lá
Fazendo o somatório de forças teremos que
Como podemos ver temos duas incógnitas ( e uma única equação (), logo de fato se trata de um problema estaticamente indeterminado. Sabemos então, que para resolve-lo precisamos do que chamamos de equação de compatibilidade.
Passo 3
Temos que lembrar que a nossa equação de compatibilidade terá como fórmula a nossa equação de deformação total, dada por
Mas onde ela será usada?
Ai que entra a nossa relação de deformação, ou seja, a deformação da nossa barra deve ser igual a deformação total máxima que ela pode ter, que pode ser dada por
O que precisamos saber primeiro: como as paredes são indeslocaveis a deformação total máxima possível para a nossa barra é zero, logo
O que devemos saber por segundo é que a deformação do trecho AD é composto de três parcelas, uma do trecho AB, uma do trecho BC e por fim do trecho CD. Logo podemos escrever a nossa equação de compatibilidade como.
Colocando tudo em termos do que já temos e também usando a nossa fórmula de deformação total teremos que
Sabemos que como a barra é homogênea, tanto a área quanto o módulo de elasticidade são iguais nos três trechos. Também sabemos facilmente determinar o valor de cada comprimento que é dado no desenho. Então o que falta é apenas determinar o valor dos normais.
Passo 4
Como só falta determinar o normal, basta apenas que cortemos as barras e façamos o equilíbrio da nossa peça.
Primeiro normal do trecho AB
Fazendo o equilíbrio teremos que
Normal do trecho BC
Fazendo o equilíbrio teremos que
Normal do trecho CD
Fazendo o equilíbrio teremos que
Passo 5
Agora que já temos os valores dos normais vamos substituir na nossa equação
Agora vamos isolar os valores de
Podemos cortar
Isolando teremos que
Agora é só calcularmos o valor de
Passo 6
Sabemos que
Substituindo teremos que
Como já sabemos qual é a nossa primeira equação, basta substituir nela para descobrimos o valor de
Passo 7
Agora que já sabemos a força em cada trecho, precisamos analisar as respectivas tensões, para isso temos que usar a nossa fórmula
Sabemos que
E a nossa área é
Sabendo todos os valores temos que lembrar que
Logo teremos que as tensões serão.
Como a nossa tensão de escoamento é podemos ver que apenas a tensão do trecho AB ultrapassa a tensão de escoamento, ou seja, todos os outros dois trechos sofreram deformações elásticas, mas o trecho AB sofrerá também deformações plásticas.
Passo 8
Como o trecho AB ultrapassou a tensão de escoamento, definimos que a tensão que calculamos é impossível e redefinimos ela como a tensão de escoamento, assim teremos que
Recalculado o normal teremos que
Mas também sabemos que, então recalculando o valor de teremos que
Esses valores devem ser guardados pois iremos usa-los novamente mais pra frente nos nossos cálculos.
Passo 9
Agora que sabemos que o trecho AB irá sofrer deformações plásticas iremos usar isso na nossa equação de compatibilidade, sabemos que
Iremos reescrever a nossa equação como
Já sabemos a fórmula que usamos para calcular as parcelas elásticas, e elas são dadas abaixo
Substituindo os nossos normais teremos que
E agora entra o maior cuidado que você deve tomar nessa questão, todos os dos normais será trocado pelo novo valor de que calculamos, não devemos de maneira nenhuma usar o primeiro valor que calculamos, mas sim o corrigido.
Com isso usaremos
Substituindo por enquanto só o valor de teremos
Vamos deixar essa equação parada por enquanto.
Passo 10
Como já sabemos que essa peça terá deformações plásticas, podemos determinar as tensões residuais que essa peça terá quando retirarmos o carregamento. Olhando o nosso diagrama de corpo livre teremos que
Sabemos que nesse caso a reação R produzira a seguinte tensão
E também produzirá a seguinte deformação
Que podemos reescrever como
Em que essa tensão é exatamente a nossa tensão residual.
Também podemos escrever a nossa equação de compatibilidade como
Com isso podemos escrever que
Com isso temos duas fórmulas para deformação plástica
Juntando as duas temos que
Podemos cortar o valor de E de todas as parcelas e isolar o valor da tensão
Isolando a nossa tensão teremos que
Sabemos que
Substituindo
Passo 11
Também disse que iria conferir a resposta através do cálculo mais rápido que já apendemos, para isso devemos lembrar que a nossa fórmula é
Em que é a primeira tensão que calculamos, considerando tudo lindo e sem deformações plásticas, e é a tensão real que definimos logo após descobrirmos que havia deformações plásticas, pra ser mais direto, a nossa própria tensão de escoamento, dessa forma teremos que
Fazendo o cálculo teremos que
Ou seja, realmente calculamos tudo coretinho sem termos nenhuma contradição.
Resposta
Ocorrem tensões residuais devido as deformações plásticas.
Exercício Resolvido #7
Elaboração própria
A barra de seções retangulares abaixo está sujeita a um carregamento P. Determine o maior valor de P que podemos aplicar nessa peça para que a mesma somente sofra deformações elásticas.
Passo 1
Nesse tipo de questão podemos ficar tranquilo quanto o cálculo que iremos fazer. Sabemos que devemos fazer uma igualdade de tensões, nesse caso igualando a tensão de escoamento com a maior tensão entre as duas seções, fazemos isso pois assim acharemos uma relação entre a carga que estamos aplicando e a tensão que fará a nossa barra deformar plasticamente. Mas aí surgem duas dúvidas.
A primeira é saber qual seção produz maior tensão, e a segunda é como trabalharemos unidades e valores, para isso temos que tomar alguns cuidados.
Passo 2
O primeiro problema é fácil solucionar, basta olharmos a fórmula de tensão normal.
Basta analisarmos o seguinte, se aumentamos a área, diminuímos a tensão e se diminuímos a área aumentamos a tensão. Ou seja, basta calcularmos as áreas e a que for menor será a que produzira maiores tensões. Sendo assim teremos que
Então sabemos que devemos usar a .
Outra coisa que podemos ver é que o normal que age na nossa peça é a própria carga P, logo teremos que
E por fim como queremos o valor máximo de P sem que haja deformações permanentes na peça, faremos
Passo 3
Agora que já temos todos os valores, devemos adequar as unidades, sabemos que
Sabemos também que a nossa área é
Ou seja, acharemos a nossa força em Newtons nesse caso, substituindo na fórmula teremos que
Resposta
Exercício Resolvido #8
Elaboração própria
Abaixo temos uma peça com 4 seções diferentes. Sabendo que ela foi sujeita a uma carga P de intensidade desconhecida e que possui , determine o máximo valor de P para que essa barra apenas sofra deformações elásticas, ou seja, fique na iminência de entrar no regime plástico.
Passo 1
Nesse tipo de questão podemos ficar tranquilo quanto o cálculo que iremos fazer. Sabemos que devemos fazer uma igualdade de tensões, nesse caso igualando a tensão de escoamento com a maior tensão entre as duas seções, fazemos isso pois assim acharemos uma relação entre a carga que estamos aplicando e a tensão que fará a nossa barra deformar plasticamente. Mas aí surgem duas dúvidas.
A primeira é saber qual seção produz maior tensão, e a segunda é como trabalharemos unidades e valores, para isso temos que tomar alguns cuidados.
Passo 2
O primeiro problema é fácil solucionar, basta olharmos a fórmula de tensão normal.
Basta analisarmos o seguinte, se aumentamos a área, diminuímos a tensão e se diminuímos a área aumentamos a tensão. Ou seja, basta calcularmos as áreas e a que for menor será a que produzira maiores tensões. Sendo assim teremos que
Então sabemos que devemos usar a .
Outra coisa que podemos ver é que o normal que age na nossa peça é a própria carga P, logo teremos que
E por fim como queremos o valor máximo de P sem que haja deformações permanentes na peça, faremos
Passo 3
Agora que já temos todos os valores, devemos adequar as unidades, sabemos que
Sabemos também que a nossa área é
Ou seja, acharemos a nossa força em Newtons nesse caso, substituindo na fórmula teremos que