Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 100

100. Resolva o problema 8.89 , incluindo o efeito de um coeficiente de resistência ao rolamento de 1,75   m m .

Passo 1

Bomm! Olha só, a primeira coisa que temos que fazer é o esboço a roda do patinete com as forças que nele estão presentes, o chamado diagrama de corpo livre:

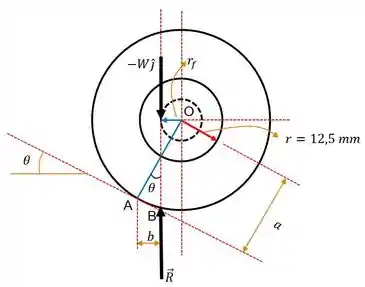
E olha só uma coisa! Do problema 8.89 , tiramos que o patinete é projetado para andar em um declive com 2 % de inclinação. Opa! Mas que beleza!

Sabe por quê? Ora bolas! Falou em taxa de inclinação, é porque falou em tangente, ou seja, obtemos que:

tan ⁡ θ = 2 100 = 0,02

Passo 2

E para condições em que estamos trabalhando com ângulo muito pequenos como é o caso aqui, nos quais b e r f são pequenos se comparado ao valor de a , podemos estabelecer a seguinte relação:

tan ⁡ θ ≈ r f + b a

Só que:

r f = μ k r

O que nos leva à:

tan ⁡ θ ≈ μ k r + b a

Sendo assim, como já temos os seguintes valores:

r = 12,5   m m μ k = 0,10 b = 1,75   m m

Vamos tratar de obter o valor de a :

0,02 = ( 0,10 ) ( 0,0125 ) + ( 0,00175 ) a

a = ( 0,10 ) ( 0,0125 ) + ( 0,00175 ) 0,02   m

a = 0,15   m = 150   m m

Por fim, como queremos o diâmetro d , basta saber que ele é o dobro de a :

d = 2 a = 2 ⋅ 150   m m = 300   m m

Resposta

d = 2 a = 300   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O carrinho, juntamente com a carga, pesa 750N( ≈ 75k g ) . Se o coeficiente de resistência ao rolamento é a = 0,75m m , determine a força necessária para puxar o carrinho com velocidade constante.
O rolo compressor tem uma massa de 80k g . Se o braço B A for mantido a um ângulo de 30 ° da horizontal e o coeficiente de resistência ao rolamento para o cilindro for 25m m , determine a força P nces
O cilindro está sujeito a uma carga que tem um peso W . Se o coeficiente de resistência ao rolamento para as superfícies superior e inferior do cilindro forem a A e a B , respectivamente, mostre que u
Determine a força P necessária para superar a resistência ao rolamento e suportar o cilindro de 50k g se ele rolar para baixo no plano inclinado com velocidade constante. O coeficiente de resistência
A barra em L se ajusta livremente em um pino de 12m m de diâmetro. Determine a força P necessária que seja apenas suficiente para girar a barra em sentido horário. O coeficiente de atrito estático ent