Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 107
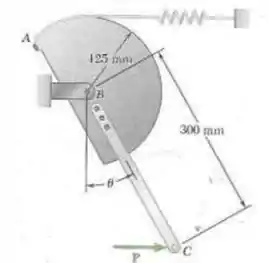
Uma força horizontal P de intensidade de é aplicada ao mecanismo em C. A constante da mola é e a mola está indeformada quando . Desprezando o peso do mecanismo, determine o valor de correspondente ao equilíbrio.
Passo 1
Primeiro, vamos usar a geometria do problema pra definir alguns parâmetros para o trabalho virtual. Se definirmos como a parcela do ângulo que se desloca, o raio do disco, temos que:
Passo 2
Sabendo que a mola está relaxada quando o ângulo é igual a zero:
Passo 3
Agora vamos aplicar o trabalho virtual para acharmos o ângulo!
Ou
Logo,
Resposta
Exercícios de Livros Relacionados
O pedal é usado para levantar uma plataforma de massa m . Determine a força P necessária, aplicada em um ângulo de 10 ° , para suportar a carga de 80k g .
Por meio de um mecanismo de cremalheira e pinhão, grandes forças podem ser desenvolvidas pelo saca rolhas mostrado. Se o raio médio das engrenagens do pinhão vale 12m m , determine a força R que é exe
A mola de constante k não está distendida quando θ = 0 . Obtenha uma expressão para a força P necessária para defletir o sistema de um ângulo θ . A massa das barras é desprezível.
Cada uma das conexões uniformes do conjunto tem massa m e comprimento b . A posição de equilíbrio do conjunto, no plano vertical, é determinada pelo binário M , aplicado a conexão da esquerda. Express
10- O cilindro hidráulico é usado para afastar as conexões e elevar a carga m . Determine a força compressiva C no cilindro, para a posição mostrada. Despreze a massa de todas as partes, a exceção de