Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 104
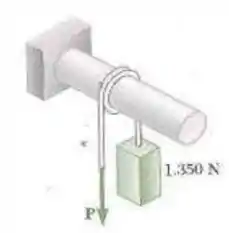
104. Um bloco de é sustentado por uma corda enrolada volta em torno de uma barra horizontal. Sabendo que o coeficiente de atrito estático entre a corda e a barra é , determine a faixa de valores de em que o equilíbrio é mantido.
Passo 1
Bom! Antes de mais nada, a primeira coisa que temos que fazer é o esboço do nosso sisteminha, o chamado diagrama de corpo livre.
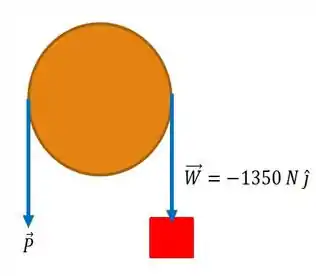
E em seguida, vamos usar a seguinte equação para problemas que envolvem atritos em correias em condição iminente de deslizamento:
Onde , é a maior tração, e , é a menor tração. Baseado nisso, temos que fazer uma análise separada para dois casos, em que é maior que ou que é maior que .
Ahhh! E o ângulo que aparece na fórmula, como a questão mesmo nos diz que a corda está enrolada volta, então é porque o nosso ângulo será:
Passo 2
a) Vamos lá! Para o primeiro caso, a maior força é e a menor força é . Ficamos então, com a seguinte relação:
Passo 3
b) Já para o segundo caso, a maior força é e a menor força é , o que nos leva à:
Resposta
a)
b)